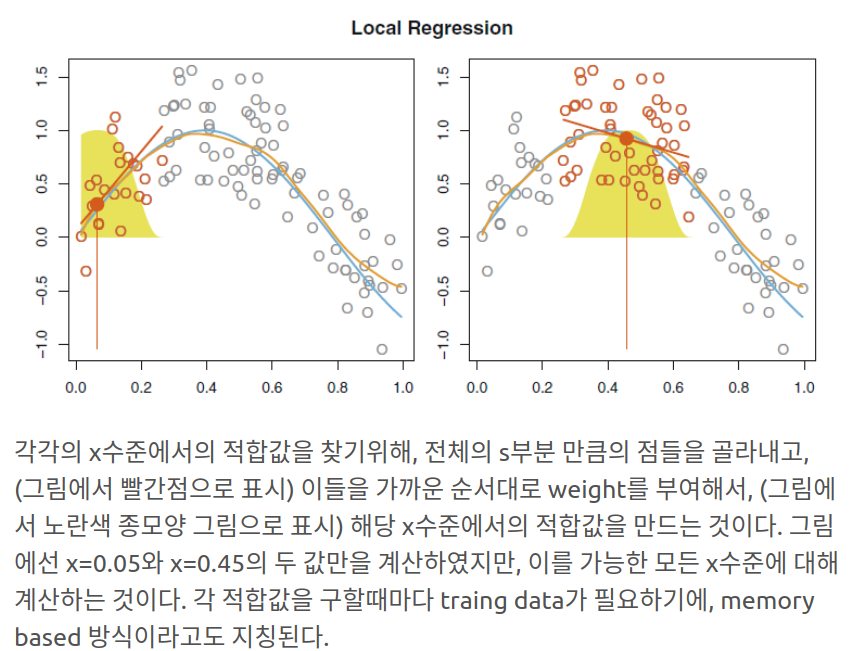
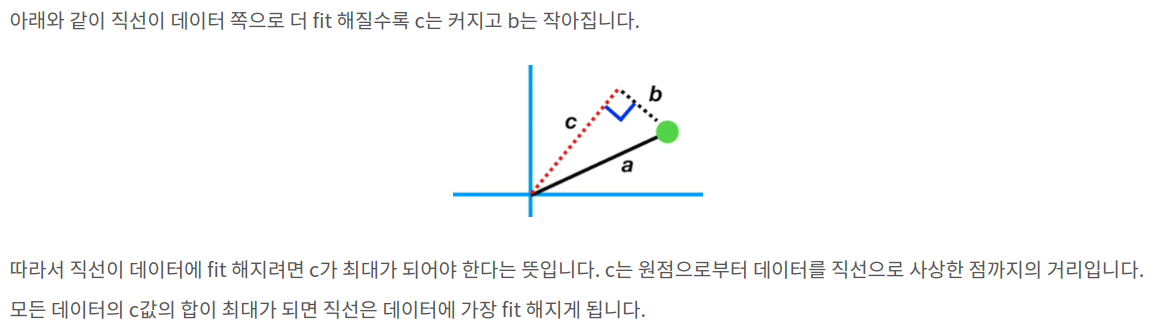
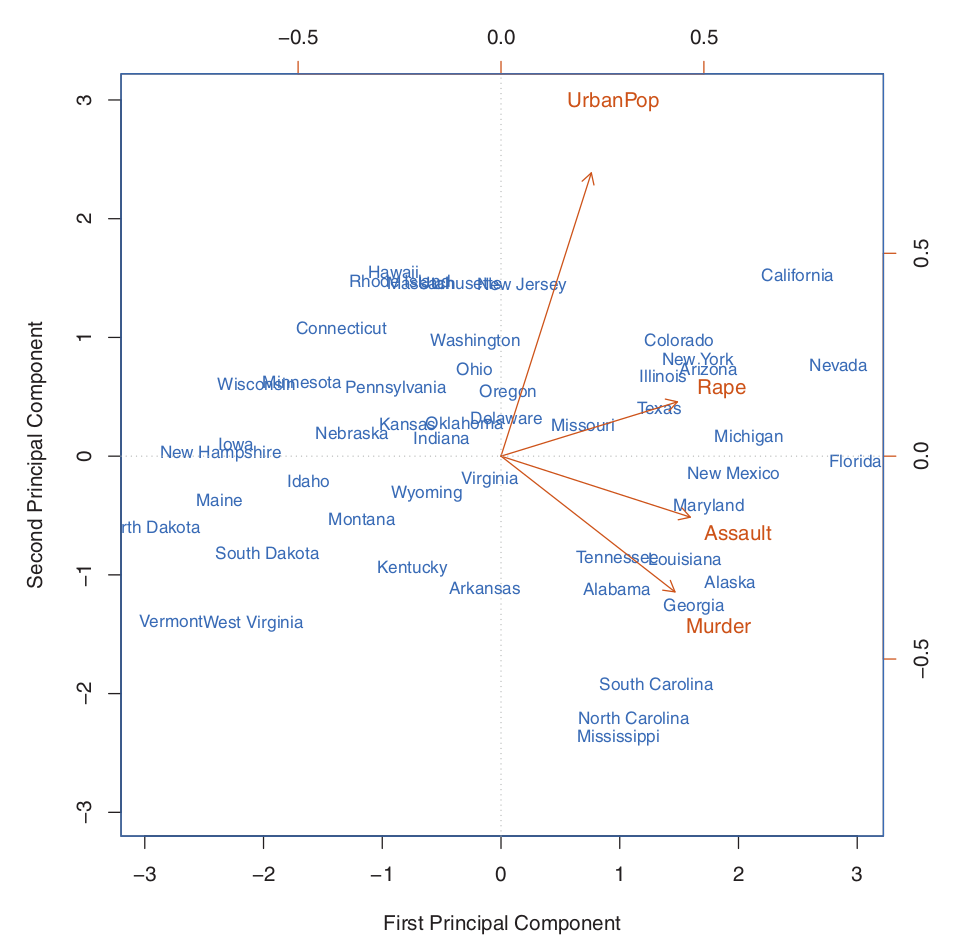
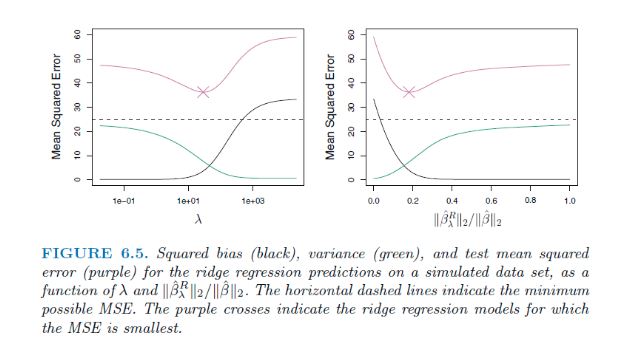
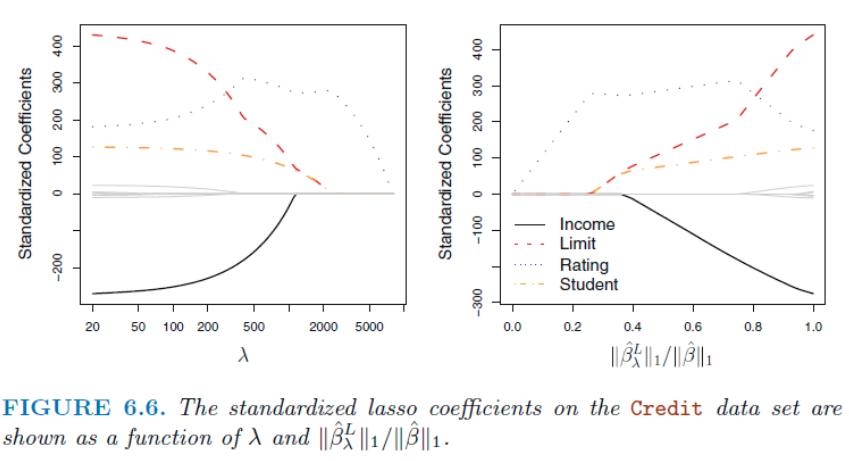
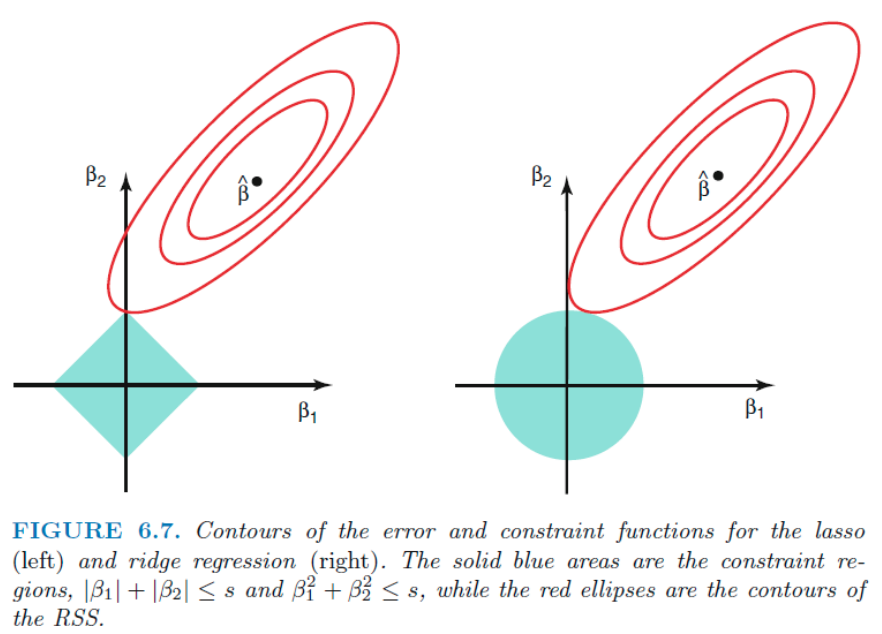
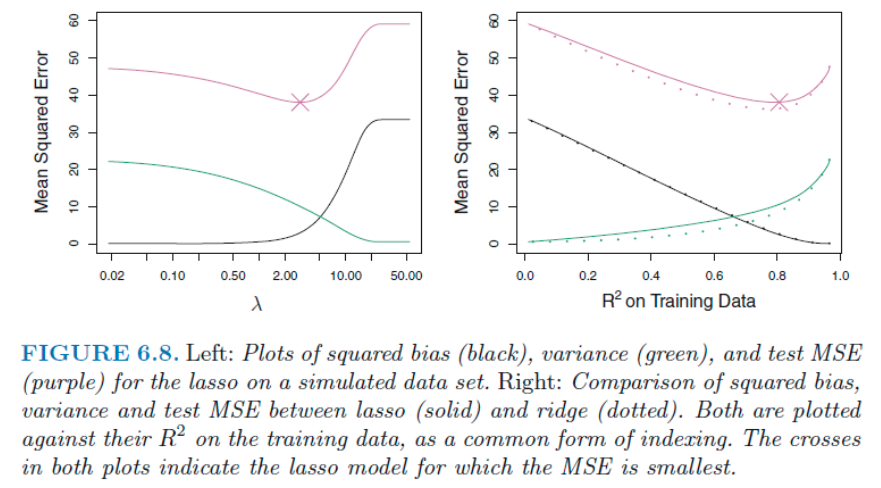
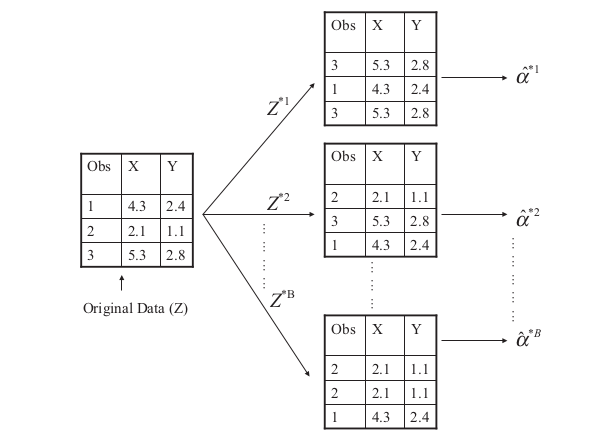
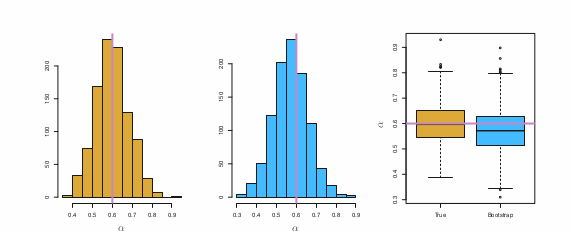
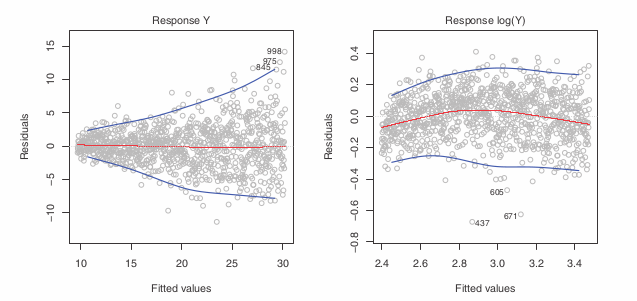
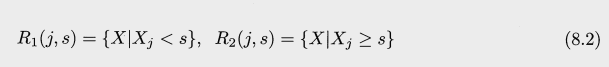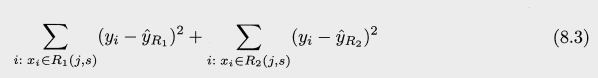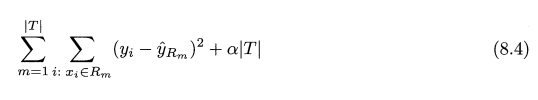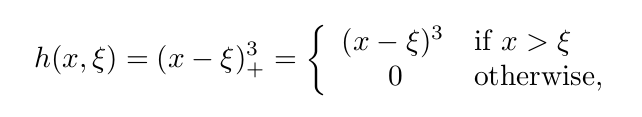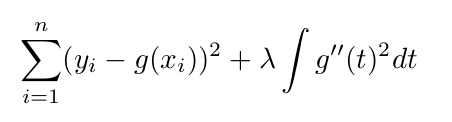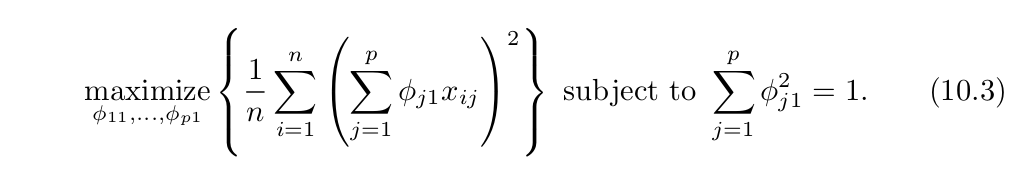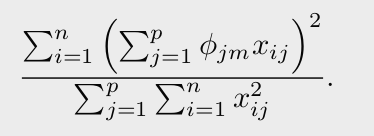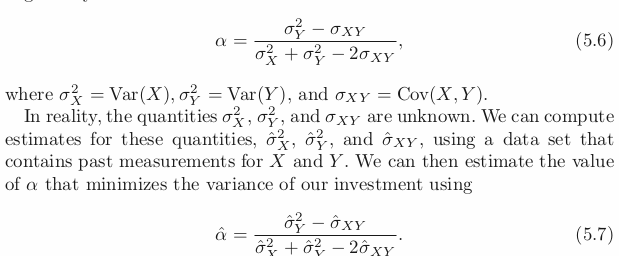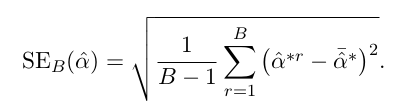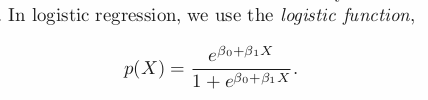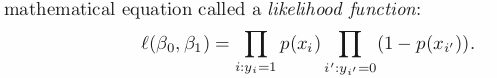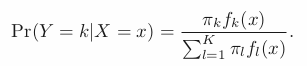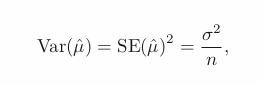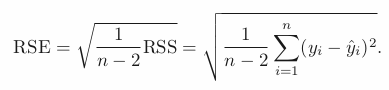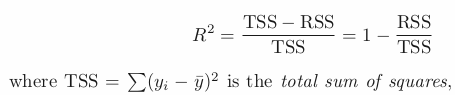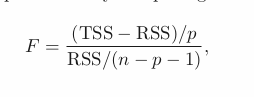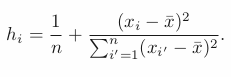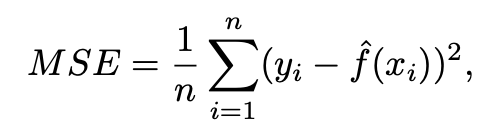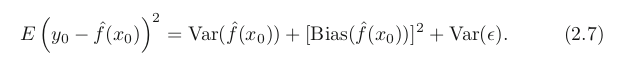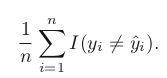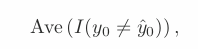Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Clustering

관측치들을 각 그룹별로 나누는데. 해당 그룹내의 관측치들은 유사하게, 다른 그룹의 관측치와는 상이하게 나누는것. 이 유사/상이 하다를 정의를 domain-specific (도메인 특정) 을 기반으로 한다

클러스터링이 비지도 (unsupervised) 방식인 이유는, 자료를 기반으로한 구조 (structure)를 발견, 그룹을 나누는것인데 비해, 지도 방식의 경우 어떠한 결과를 유추/예측 하고자 하는것.

Clustering AND PCA 모두 summary를 통해 데이터를 간단하게 하려 하지만

• PCA: 분산의 많은 비율을 설명하는 관측치들을 저차원 표현으로 찾으려 함
• Clustering: 관측치들중 같은 서브그룹을 찾으려 함.

즉 클러스터링은 사람들 (관측치)들중 이 제품을 잘 살것같은 그룹을 찾아내는 형식 - market segmentation 이라고도 한다.

K - mean clustering

미리 지정한 수의 클러스터로 나누는것.

이 k 개의 클러스터간 서로 절대 겹치지 않으며 모든 관측치들은 어느 한 클러스터에 속해있다.

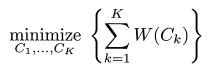
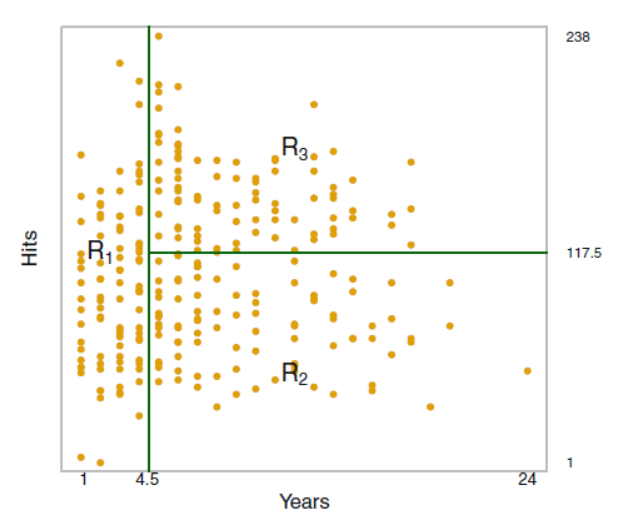
위의 식에서 유추할수 있듯, 한 클러스터 내에서의 변동이 가장 적은 클러스터링을 목표로 하고 있다.

이 변동 W(Ck) 를 정의 하는 방법은 여러가지 이지만 가장 일반적으로 유클리드 거리 제곱 (squared Euclidean distance)를 사용한다. 이를 적용하면 위의 식이 다음과 같이 변한다.

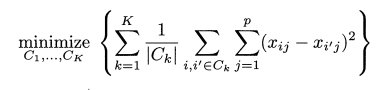
Ck = 클러스터내 관측치들의 수. 관측치들 사이의 pairwise한 거리의 제곱의 합을 관측수로 나눈것.

물론 위의 모든 방식을 사용하려면 K ** n 개의 분할 방법이 존재하기에 다음과 같은 알고리즘을 사용한다.

즉 랜덤하게 클러스터를 분배하고, 각 클러스터의 관측치들의 centeroid 를 벡터 중간값으로 정한후, 가까운 클러스터로 다시 재분배, 반복하는것. 해당 재분배가 (클러스터의 변화가) 없을때가지 반복하는것.

물론 이러한 방식은 초기 클러스터가 어떻게 분배 되느냐에 따라 달라지는 국소 최적 (local optimum) 이다 따라서 이를 피하기 위해 랜덤 할당을 다르게 해서 여러번 실행해보고, 위의 식의 값이 가장 작은것을 선택한다 ( = gloabl optimum) K 숫자 선택은 이후에 다뤄진다.

Hierarchical clustering

K-mean clustering 이 가지고 있는 단점: K 를 미리 지정해야 한다 이 없는 방식이며, dendrogram 이라고 하는 tree-based 로 표현한다

bottom-up (위로) and agglomerative (융합) 클러스터링을 설명하는데 이들은 가장 보편적인 계층적 클러스터링 ‘방식이다.

해석

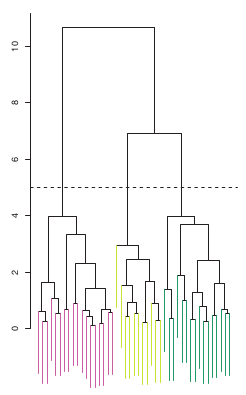
밑의 (잎) 이 위로 올라가며 가지로 융합되는 모습이다. 이 융합되는 트리의 높이가 낮을수록 관측치간의 유사성이 더 높음을 뜻한다. 또한 그림으로 한눈에 다른 색 (다른 그룹)이 서로 융합되는 높이를 알수도 있다. . 위의 그래프의 경우 초록 노랑의 융합이 빨강보다 더 빠르기에 초록 노랑이 더 유사함을 알 수 있다.

주의할 점은 이 관측치의 유사성은 수평 (즉 옆에 가까이 있냐) 수준이 아닌 수직 (융합이 언제 일어나느냐) 로 판단해야 한다. 덴드로그램을 절단하는 수평선이 곧 k의 수이다. 위의 그래프는 5에서 절단함으로써 3개의 클러스터링을 얻는다.

다만 덴드로그램은 TREE 이기때문에 2개씩으로 밖에 나눌수가 없음. 즉 프랑스미국영국을 나눌때 프랑스 | 미국영국 이후 프랑스 미국 영국 과 같이 두번에 걸쳐 3번에 나눈다. 결국 각각의 다른 그룹이 2번에 걸쳐 나눠지는 이러한 형태때문에 가끔 k-mean clustering 보다 정확도가 낮은 결과를 나타낼수 있다.

알고리즘

각 관측지의 페어마다 비유사성 (dissimilarity)를 정의한다 (유클리드 거리를 가장 많이 사용).

덴드로그램 바닥의 n 개의 관측치에 n 개의 클러스터를 주고, 가장 가까운것끼리 합쳐서 결국 1개의 클러스터가 될때까지 진행한다.

위의 알고리즘은 문제를 가지고 있는데, 여러 관측치를 가지고 있는 클러스터간에 비유사성은 어떻게 정의 하는가 이다. 이를 해결하기 위해 완전연결 평균연결 단일연결 무게중심연결을 사용하는데 보통 평균,완전. 단일을 많이 사용한다. 평균,완전 연결이 균형잡힌 덴드로그램을 제공하는 경향이 있어 더 선호된다.

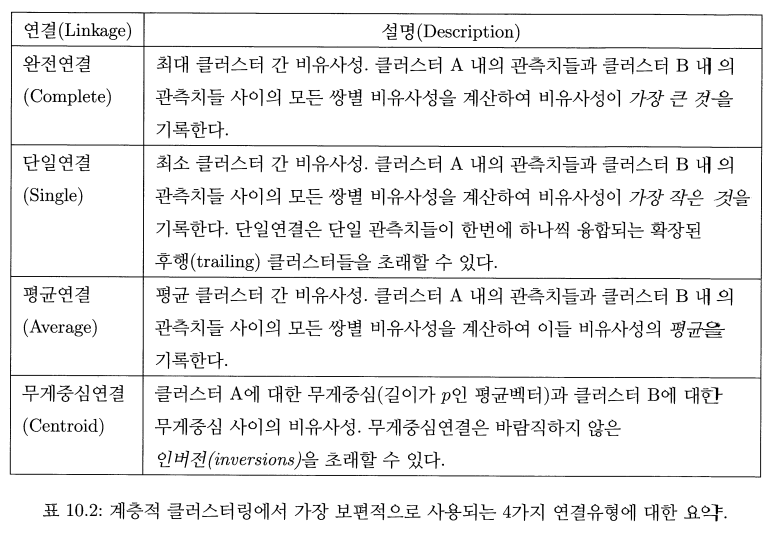
비유사성 측도

현재까지 유클리드 거리를 사용했으나, correlation-based distance 같은 방법은 상관성만 높다면 거리가 떨어져있어도 유사하다고 간주하는 방법이다. 즉 유클리드는 소비자가 구매한 양끼리 묶어서 클러스터링을, 상관 기반 거리는 비슷한 물품을 구매한 소매자끼리 묶는 방식이다.

또한 비유사성의 경우 표준편차가 1이 되도록 스케일링을 고려해야 할 수 있다 (단위차이를 없애기 위해)

이슈

클러스터링은 매우 유용하지만 여러 이슈도 존재한다.

큰 결과 작은 결정 (small decision with big consequences)

• 표준화과 진행되어야 하는가? 평균 = 0, 표준편차 = 1 이 되도록 스케일링 되어야 한다등등
• 계층적 클러스터링의 경우
  • 어떤 비유사성 측도를 사용할것인가
  • 어떤 연결을 사용해야 하는가
  • 어디서 덴드로그램을 절단해야 하는가
• K-평균 클러스터링의 경우 몇개의 클러스터를 사용해야 하는가

이러한 작은 결정들은 결과에 큰 영향을 미친다.

검증

찾은 클러스터들이 단지 아웃라이어 (노이즈)의 결과인지 아니면 진정 어느 한 부분그룹을 대표하는 (나타내는) 클러스터인지 검증해야 한다. 이를 위해 p값을 할당하는 기법들이 존재하지만 무엇이 딱 좋다 말할수는 없다

다른 고려사항

k-mean clustering and 계층적 클러스터링 모두 각 관측치에 하나의 클러스터를 할당한다. 이러한 행동은 outlier 들의 존재로 클러스터가 심하게 왜곡될수 있다. mixture model 은 이러한 특이점을 수용하는 방법인데 k-mean clustering 의 soft 버전이라고 할 수 있다.

또한 클러스터링 방법은 작은 변동 (perturbations)에 robust 하지 않다. 이는 n개의 관측치에서 몇개를 제외하고 클러스터링을 다시 진행하면 보통 그 전의 클러스터링과 유사하지 않다.

결과 해석및 접근 방법

위의 이유들로 인해 여러번 클러스터링을 하고, 지속되는 패턴을 찾는것이 좋다. 클러스터링이 얼마나 robust 한지 감을 잡기 위해 부분관측치에 대해 클러스터링을 수행하는것도 좋다.

중요한점은 분석결과인데, 이러한 결과로 인한 결과는 절대적으로 신뢰해서는 안되며, 단지 가설 개발에 이용되어야 한다.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Why?

Tree-based는 regression과 classification을 위한 방법으로, 예측변수의 전체 공간을 단순한 여러 영역으로 계층화 (stratifying) 혹은 분할 (segmentation)하는 방법이다.

예측: 해당 영역의 training data의 평균값이나, 최빈값에대해 예측한다

이 방식은 단순하고 설명력이 좋은 반면에, supervised (chapter 6,7)에 비해 예측력이 떨어지나, 이를 보완하기 위해 bagging, random forests, boosting과 혼합하는데, 위의 방법들을 사용하면 다중트리 (multiple trees) 드링 생성된다. 이 다중트리는 합의 예측을 제공하기에 나중에 하나로 결합된다. 이로 인해 예측정확도의 엄청난 상승을 가져온다. 하지만 이로 인해 해석이 다소 어려워질 수 있다.

Decision Trees

Decision Tree는 regression and classification 모두에 사용된다

Regression Trees

각각의 노드 (R1,2,3)들은 terminal nodes or leaf of tree 라고 부르며 그 전까지의 노드들 (리프가 아닌 중간 단계)은 internal node 라고 부른다.

위에서 보면 알 수 있듯, 메이저리거의 경우 년차가 연봉을 정하는데 가장 중요한 역할을 하고 있음.

이처럼 Decision Tree는 설명력 측면에서 강점을 가지는데, 위의 그림으로 시각적 설명이 가능하다.

Prediction via Stratification of Feature Space

1. 모든 X (변수) 가 포함된 공간을 J 개로 겹치지 않게 나눈다

   1. RSS를 최소화 하는 방향으로 위의 그림처럼 박스형식으로 쪼갠다.

   2. 물론 무한한 박스 조합이 가능하기에 Top-down or greedy 방식을 사용한다.

      1. 당장의 RSS를 최소화 하는것을 목표로 한다 (greedy) - recursive binary splitting 이라고 칭한다.

2. s 는 cutpoint 로 RSS가 최소화 되도록 영역을 밑의 두가지로 분할하는 점이다.

   

3. 다음의 식이 최소화 하는 j (공간 갯수) 와 s를 찾는다

   

   5. 위의 첫 식으로 만들어진 두 영역중 하나를 선택해 같은 방식을 적용하여 3개의 영역이 된다. 이와 같은것을 계속해서 반복하며, 설정해둔 stopping criterion 을 만족할때가지 진행한다. 예를 들어 한 영역당 관측치가 5개 이상이어야 한다등의 조건.

4. 각 공간에서 training data 평균을 통해서 일관된 예측값을 반환한다. 모든공간에 같은 예측을 시행한다.

Tree Pruning

위의 방법은 훈련셋에 좋은 예측이 가능하지만, 데이터 overfit의 가능성이 높은데 이는 지나치게 세분화된 tree는 training set 의 특징또한 포함할 수 있기 때문이다. 이로 인해 test set에서 성능이 좋지 않다.

분할 수가 적다면 편향성이 약간 증가하지만 분산이 낮아져 해석하기 쉬울것이다.

위에서 설명한 방법을 보완하는 방법은 어느 threshold 까지만 리빌딩일 진행하도록 하는것. 이는 작은 트리를 (분할 수가 더 적은) 만들수는 있지만 short-sighted (근시안)적인데 왜냐면 초기에는 좋지 않아 보인 분할이 나중에 가면 좋은것일수도 있기 때문이다.

더 나은 방법은 큰 트리 T0 를 만든뒤 이 트리를 다시 prune 하여 subtree를 얻는것. 그렇다면 어떻게 prune 하는것이 좋은 방법인가? - 최종 목표는 lowest test error 를 갖는 subtree를 찾는것이지만 이에 대해 모든 CV는 불가능 하다.

이를 위해 Cost complexcity pruning (or called weakest link pruning) 을 사용한다. 가능한 모든 서브트리를 고려하는것이 아닌 조율 parameter a 로 다음식을 최소화 하는것

T = num of Terminal node, R_m = box corresponds to mth terminal node, hat(y)R_m = R_m 훈련 관측치들의 평균. a = 0 일 경우 subtree T = T_0.

1. 각 terminal node 에서의 RSS 를 줄여주는 loss-term (앞부분)
2. 지나치게 많은 terminal node 가 없도록 (복잡성늘 낮춰주는) penalty form (뒷부분)

위 두가지의 폼을 a로 비율적으로 조정하는것인데 이 a를 CV를 통해 구하는것.

최종 알고리즘

1. 모든 자료들을 이용해서 resursive binary split 계속해서 진행하여 stopping criterion 만족하면 멈춤 (full size tree) 이는 a = 0 일때의 트리와 같다.
2. 이렇게 최종적으로 만들어진 트리에 cost complexity pruning 을 적용하여 가장 좋은 서브트리들을 a의 함수로 얻는다.
3. K-fold 를 진행하며 a를 선택한다.
   1. 모든 훈련자료의 kth fold 의외의 fold 에 위 1,2번 반복
   2. kth fold 를 이용하며 나머지에 error 를 평균내서 validation error 가 가장 낮는 a로 결정한다
4. 3번에서 구한 a를 통해 1번의 트리 (처음 큰 트리) 에 pruning 을 진행한다 - 그러면 가장 좋은 서브트리를 선택한다!

Classification Tree

For a classification tree, we predict that each observation belongs to the most commonly occurring class of training observations in the region to which it belongs. 가장 많이 등장한 클래스로 분류. 따라서 클래스 비율또한 관심을 가진다.

recursive binary splitting 을 classification error rate 를 이용하여 시행한다.

Pmk = kth class에 나온 m 번째 영역내의 훈련 관측치들의 비율

1 - (m 영역에서 여러 k들중 가장 많이 등장한 비율). 하지만 클래스간의 비율을 고려하지 않아 좋은 식은 아니다. 이를 보안하기 위해 Gini index or entropy를 이용한다.

지니는 impurity를 가장 낮게 가지는 클래스를 선택하여 진행한다. 마찬가지로 교차 엔트로피또한 m 번째 노드가 pure 할 수록 impurity 지수가 낮을것이고, 그것을 선택한다.

최종 pruned 된 트리에 대한 예측 정확도의 경우 위의 classification error rate 방법을 사용한다.

양쪽 모두 Yes (left: 7/11, right: 9) 인데 이는 지니와 엔트로피의 purity를 올려주기 때문에 분할한것. 즉 두개다 모두 Yes 이므로 분류오차를 줄여주지는 않는다.

Tree vs Linear Models

선형이라면 선형회귀,아니면 트리. 결국 때에 따라 다르다 맨위의 경우 선형이, 아래의 경우 트리가 더 좋은상황.

Pros and Cons of Trees

Pros:

• 설명하기 매우 쉽다 (linear 보다도)
• 인간의 의사결정 과정을 더 밀접하게 반영한다고 생각된다
• 그래픽으로 나타내기 쉬우며, 비전문가 또한 쉽게 해석 가능 (물론 크기가 작으면)
• 더미 변수를 만들지 않고서도 qualitative, quantatative 모두 가능

Cons:

• 예측 정확도가 좋지 못하다 - prune을 하더라도 overfit의 한계를 벗어나지 못하기 때문.
• ‘non-robust’ - 데이터의 작은 변화에도 트리의 최종 예측값이 크게 변동한다 (variance가 크다)

예측 정확도를 bagging. random forest, boosting 을 하여 향상 시킬수 있다.

Bagging & radom forest & boosting

Bagging (Bootstrap aggregation)

bootstrop 을 활용한 방식. Decision Tree 는 high variance (non robust) 하다는 단점을 가지고 있다. bagging 을 사용하여 variance를 낮추는것.

분산을 줄여 예측 정확도를 증가시키는 자연스러운 방법은 population으로 무터 많은 수의 training set 을 취하여 각각의 training set 별로 예측모델을 만든후, 이 예측결과들을 평균내는것. 물론 이 처럼 다수의 훈련셋은 보통 불가능 하므로, 붓스트랩을 사용하여 표본을 샘플링, 훈련자료들을 생성하는것.

말 그대로 bootstrap 하여 (자료를 만들어서 예측하고) aggregating (평균내는것) 하는 방법.

Regression tree의 경우:

붓스트랩하여 훈련셋 B개를 만들어 B개의 regression tree 를 만들고, 이 예측 결과들을 평균낸다. tree 들은 prune 되지 않은 큰 트리들이다. 따라서 각각의 훈련 tree 들은 분산은 크되 편향이 작은 상태. 이 처럼 분산이 크고 편향이 작은 나무들을 모두 모아 평균하여 분산과 편향이 작게 만들어주는것.

Classification Tree의 경우:

똑같지만, B 개의 나무에 의해 예측된 클래스를 기록하여 이 예측간에 가장 자주 발생하는 클래스를 선택하는것.

• Out of bag Error Estimation
  • Bagging 은 bootstrap에 의해 복원추출에 뽑히지 않은 데이터들 (보통 1/3가 안뽑힘) 이 자동으로 validation set 되어 CV를 하지 않아도 test error의 추측이 가능한데. 이 뽑히지 않은 데이터들을 out-of -bag (OOB) 라고 부른다
  • 즉 뽑히지 않은 B/3 개의 모델들이 특정 데이터에 예측을 하고, 이 예측들을 평균낸다. 이 방법으로 OOB error and Classification error 를 구할수 있다.
  • B가 클경우 OOB 오차는 LOOCV의 오차와 사실상 동일하며, CV가 힘들만큼 데이터가 클때 유용한 방식이다.
• Variable Importance Measures
  • 여러 나무를 합하여 예측력을 올렸지만 (분산을 줄여서), 이로 인해 해석력을 잃었음. 왜냐면 이제 나무 한개가 아니니까.
  • Bagging 전만큼은 아니지만 RSS (regression), Gini Index (classification) 를 이용하며 전반적인 예측변수 중요도를 확인할수있다.
  • 모든 B개의 나무에대해 각 변수에서의 split으로 인한 RSS/Gini 가 감소한 정도를 측정하여 평균을 낸후, 가장 많이 감소하였으면, 해당 변수가 중요하다는것.

Random Forest

Bootstrap은 샘플링을 통하기에 correlation 이 높다 (서로 비슷한 모델이라는 뜻). 이로 인해 covariance가 높고, 그렇기에 bagging으로 인한 variance 감소가 크지 않다. Correlation을 줄인 bootstrap 방식이 바로 random forest 인것.

• 똑같이 bootstrap을 통해 B개의 나무를 생성한다. 하지만 split 할때 전체 p개의 예측 변수중 랜덤하게 m 개만 골라서 그 중에 또 split 기준을 만든다. 이후 계속해서 반복한다. 보통 m^2 = p 이다.
• m개는 결국 p개의 반도 안된다. 이는 한개가 강력하고 나머지는 적당한 예측 변수를 가정한다면, bagging 의 경우 모두 나무가 비슷비슷 하기에 가장 강력한 변수를 top split으로 뽑을것이고, 이로 인해서 bagged tree들이 모두 비슷해지는 효과를 만드는것. 앞에서 말하였든 highly correlate 된 통계를 평균 내는것은 correlate가 약한것들의 평균으로 얻는 variance감소보다 더 적다
• 이와 같은 현상을 피하기에 랜덤으로 뽑아서 다른 예측변수들도 (기회를 얻는것) 사용되게 하여 bagging 보다 결과적으로 decorrelate한 효과를 가지는것. 따라서 이 나무들의 평균으로 얻는 variance 감소가 훨씬 커진다.
• m = p 는 결국 random forest = bagging 이며 많은수의 변수들이 correlate 라면 sqrt(p)보다 더 적은 m 이 유효할 수 있다.

Boosting

강력하지는 않으나 보완에 초점을 맞춘 약한 모델 (weak leaner)를 결합해서 정확하고 강력한 모델 (strong leaner)를 만드는 것. 다른곳에서도 사용가능하나 decision tree만 이야기한다

Bagging 의 경우 bootstrap을 이용하여 데이터셋을 만든후, 개별적인 decision tree 생성인데 이 생성과정이 서로 관련이 없고 독립적이다. boosting 의 경우 tree들이 순서대로 만들어지는데, 각각의 tree는 이전 트리들의 정보를 이용하여 만들어진다. 즉 boosting 은 bootstrap sampling 을 사용하지 않는것. 대신 각 트리는 수정된 버전의 원래 데이터셋에 적합한다.

맨 처음에만 데이터에 적합을 하고, 그 이후부터는 이전 tree 의 residual에 적합하는것.

즉 boosting 의 경우 slowly learning method 이다.

Boosting tree에는 3가지의 hyper parameter 가 존재한다.

• Tree의 갯수 B: Boosting 은 variance 감소가 목적인 bagging 과 다르게 bias를 줄여나가는 방식이다. 따라서 B가 너무 크면 overfit이 될 수 있다. B 는 CV 를 이용하여 선택한다
• 반영비율 lambda: 각 step에서 배운것을 얼마나 반영할지 정해주는것. 보통 0.01/0.001 을 사용한다. 람다가 작을수록 더 큰 B 가 필요하다 (왜냐면 람다가 작다 = 매 스텝에서 (그 전 트리에서) 배우는것이 적다).
• Tree 의 split 갯수 d: boosting complexity 를 조절해준다. Complexity가 높으면 flexible하고 이는 variance 가 높고 bias가 작음을 의미한다. 위에 말하였는 boosting은 bias를 줄이는데 목표를 두고 있기에 complexity가 크지 않다 (왜냐면 overfit 위험이 생기니까). 때로는 d = 1 일때가 좋을수도 있는데, 이는 addtive model에 적합하기 때문. d = interaction depth라고 생각할수도 있는데 선형회귀의 X1X2 같은 여러 변수의 조합을 고려하는 tree node가 생기기때문.

Boosting 은 이전 모델의 실수를 기반으로 만들어지기에 각각의 트리들이 작은 트리여도 충분한 경우가 많다.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

선형 모델: 모델의 단순성으로 해석과 추론이 쉽다는 장점. 하지만 이러한 가정한 현실적인 문제에 대한 예측을 하기에는 터무니 없는 가정.

따라서 이와 같은 선형가정을 완화시키되, 해석과 추론력을 최대한 잃지 않는선에서 예측력을 증가 시키는 방법들에대해 배워본다.

1. Polynomial Regreisson: 다차항을 이용하여 선형 모델을 확장
2. Step function: K부분으로 변수를 나누어서 constant를 생성하는 방법
3. Regression splines: 위 1,2 방식의 확장으로 K부분으로 나누어 각 부분에 다차항을 적합하는 형식이다. 각 부분은 양 옆의 범주에 대해 매끄럽게 만들어야 한다는 제약이 있지만, 적당한 범주로 나눈다면 유연한 적합이 가능하다
4. Smoothing penalty: 위 3번과 비슷하지만 매끄럽게 한다는 제약을 최소화 시키는 방식
5. Local Regression: 3,4 번과 비슷하지만, 각 범주가 겹칠수 있다. 이로 인해 유연한 적합이 가능한것
6. Generalized additive model: 여러개의 예측 변수들에 적용하는 방법

Polynomial Regression

예측변수의 전체 구간에 non-linear 형태를 부여하는 방식

단순하게 각 변수를 다차항의 형식으로 넣어준 방법이다. X2 = X1 ^ 2 과 같은 형식.

일반적으로 3,4차 이상으로 포함시키지는 않는다.

왼쪽: Least Square 4차 적합. 오른쪽: 왼쪽의 250이상의 고소득자에 대한 Logistic 4차 적합. 점선들은 예측값의 분산을 통해 구한95%의 confidence interval

예측값의 분산은 다음과 같이 구할 수 있다

Logistic의 경우 확률을 반환한다는것을 기억하자. 고소득층에 대한 데이터는 79개에 불과하여 신뢰구간이 매우 넓게 나옴을 확인할 수 있다.

Step Functions

전체 X를 몇개의 구간으로 나누고 일정한 상수를 부여하는 방식

절편인 b0 는 Y값의 평균이고, 나머지 b 들은 각 구간에 속한 데이터의 평균과 b0와의 차이를 의미하게 된다. C1 ≤ X ≤ C2의 평균값 - b0 = b1. 이러한 각각의 계수들은 마찬가지로 least square로 적합하여 구한다. 각 더미 변수에 대한 (C들은 더미 변수이다) 분산/신뢰구간은 3장 참조

예측값에 자연적으로 부분을 나눌수 있는 지점이 존재 하지 않는다면, 이 방식은 옳지 못한 방향을 나타낼 수 있는데, 명확하게 증가 추세인 구간을 제대로 구분지어주지 않는다면, 이 증가 추세를 반영하지 못하기 때문이다. 위 그래프에서 나이가 들수록 월급이 올라가는 증가 추세를 반영해주지 못한 상황이다.

Basis Functions

앞의 두 방식은 Bisis funciton의 특별한 형태라고 볼 수도 있다.

앞선 두 방식과 다르게, 선형 모델로 X를 적합하지 않고 다음과 같은 모델에 적합한다.

각 b의 값은 이미 정해져 있으면 알려진 상태임을 명시하자. 이 말인 즉, 우리는 사용할 함수를 미리 선택해 놓는다는 의미이다.

Regression Spines

Piecewise Polynomials

맨 위 1번 Polynomial regression 처럼 전체 X에 대한 다항적합을 하는 형식이 아닌 몇개의 범주에 대해 비교적 낮은 차수의 적합을 따로따로 하는것을 piecewise polynomial regression 이라 한다.

계수가 바뀌는 지점을 knots 라고 하는데 (서로 다른 부분을 묶는거니까) 삼차 다항식에 이 knots가 없다면 결국 그건 그냥 보통의 평범한 삼차항이다. 다음은 knots가 한개 존재할때의 3차항이다.

즉 c를 기준으로 2개의 부분으로 나누어 각각의 부분에 다항적합을 한것이다. 이 모델의 degreef of freedom = 8 이다 (각각 4개씩)

하지만 이 형식은 중간의 knots 들을 부드럽게 연결하는 제약이 없기때문에 다음과 같은 말도 안되는 모델이 탄생하게 된다 (1번).

Constraints and Splines

1번의 그래프에서 나이가 50일때 갑자기 월급이 폭등하는 것은 말이 안된다. 이에 50부근의 선들을 연결해 준 그래프가 2번이다 (continuous piecewise cubic). 하지만 이 또한 꺽인듯한 부분을 볼 수 있는데 이러한 약한 제약을 (50 부근 이어준것) 가지고는 다른 그래프에서 v자 형태로 나올수 있기에 고쳐주어야 한다. 이 부분을 부드럽게 해주기 위해 1,2차 미분을 해주어야 한다. 즉 50부분에서 continuous + smooth (1차 2차 미분) 라는 세 가지의 제약을 적용한것이 3번 그래프.

이러한 제약은, 자유도를 하나씩 잃음을 의미한다. 따라서 1번에서는 자유도가 8, 2번에서는 7, 3번에서는 5이다. 보통 cubic spline uses 4 + K df (K = num of knots).

Splines Basis Representation

d차 적합을 하면서 d-1차 까지의 미분을 달성하기 위해서는 basis function 을 올바르게 선택해야 하는데, 이는 trucated power basis funciton 을 이용하면 된다.

다음은 cubic spline을 cubic regression에서 만드는 방법이다.

위의 뱀처럼 생긴것이 knot을 의미한다. 위의 식을 각 knot마다 추가하는것이다.

하지만 위와 같은 방식으로 구할 경우, 양 끝에서의 예측 신뢰구간이 넓어지므로 예측의 정확도가 떨어지는 현상이 나타난다. 원래 모든 모델의 분산은 양 끝에서 커지지만 non-linear 적합을 시도한 이 경우에 (which has more flexibility) 분산이 더 커지게 된다.

이러한 현상을 고치기 위해 맨 양쪽의 knot 이후에 있는 부분의 경우 선형 적합을 하여서 문제를 완화시키는데 이를 Natural Cubic Spline이라 한다.

위의 그래프를 보면 수직 점선 (knot) 이후에 빨간 점선이 분산을 적게 가지고 있음을 볼 수 있다. 이러한 양끝쪽에 3차 적합이 아닌 1차 적합을 하기에 자유도를 2씩 잃어서 K+4-(2*2) = K df.를 가지게 된다.

Num and Location of the knots

이제 knot를 어떻게 사용하는지 알았으니 몇개를 어디에 사용해야 하는지를 알아야 한다.

적정한 df를 설정하고, 이에 따른 균등한 quantile에 knot를 배정하는 형식.

결국 df (자유도)를 몇으로 설정하지가 문제인데, Cross-validation을 이용하여 CV-error 값이 가장 낮은 자유도의 갯수를 사용한다

Comparison to Polynomial Regression

보통 Polynomial Regression의 경우 flexible 하기 위해 차수를 엄청나게 높이고는 하는데, 반대로 regression spline의 경우 차수는 유지하되, knots를 늘리는것으로 유연해진다. 따라서 대부분의 경우 regression spline이 produces more stable estimates. 또한 급변하게 변하는 부분에 대해서 우리가 따로 더 많은 knots를 부여함으로써 (반대로 원만하면 knots 수 줄이고) 유연성을 적절하게 조절 할 수 있기에 더 좋다.

위의 polynomial의 경우 15차 항인데, 이로 인해 끝쪽이 매우 요동친다.

Smoothing Splines

Overview of Smoothing Splines

Regression과 다르게 Smoothing은 모든 x에 knots를 두기에 갯수나 위치 지정의 문제가 없다!

결국 우리가 원하는 사항은 RSS를 작게 만들면서, 부드러운 함수를 찾는것.

위 식의 왼쪽 부분이 RSS이다. 이러한 형태는 Loss (잘 적합) + Penalty (변동이 크지 않게) 식인데, Lassor and Ridge에서 사용되었던 형태와 비슷하다.

오른쪽의 식은 t부분에서의 변화도를 나타내주는데, 변화도가 음수일 경우도 있으니 제곱을 해준다. 람다 값이 커질수록 더 부드러워질것이다.

람다가 0이면 모든 데이터를 지나가고, 무한하다면 선형 (굴곡이 없는 직선 - 선형회귀와 같다). 결국 람다 = bias variance trade off 정도를 조정하는 값인것이다.

이 람다가 3차에서 최소화 될때는 위에서 이야기 했던 2차 미분이 가능한 knot를 가지고 양 끝이 linear 한 natural cubic spline이다. 물론 이와 정확히 같은 값의 식이 나오는게 아니라, 비슷한 형식의 shrink된 함수

Choosing lambda

In smoothing spline, lambda controls the smoothness. Hence, the effective degrees of freedom changes depending on the value of lambda. 람다가 0에서 무한까지 변할때 effective df는 n에서 2까지 변한다.

기존의 자유도는 pramater의 갯수로 계수의 수를 뜻했다. 따라서 smoothing spline은 명목상 n개의 자유도를 가지고 있지만, 이들인 이미 shrink 되도록 constrain (제약)을 받고 있기에, 이 제약의 정도에 따라 flexibility가 다르다. 따라서 정확히 어느정도의 자유도를 실질적으로 가지고 있는지를 나타내주는것.

Regression 과는 다르게 람다를 어느 값으로 할지가 남아있다 (RSS를 최소화 하는). 물론 Cross-validation 을 이용한다.

임의로 정한 effective df 인 16에 비해 계산으로 나온 6.8 이 거의 유사한 형태를 보여주고 있다.

Local Regression

각 특정 타겟 포인트 근처의 관측 자료들만을 토대로 적합시켜 flexbile하게 하는 방식

위에서 중요한 사항은 얼마나 많은 이웃들을 볼것인지 즉 s를 몇퍼센트로 설정할지이다. s가 작을수록 더 지역적인 (조그만) 부분으로 꾸불한 선이 나올것이다 물론 이 s 또한 cross-validation 을 통해 찾는다.

Local Regression은 p-차원에서 p가 3이나 4보다 훨씬 클 경우, 굉장히 안좋은데 이는 대체로 트레이닝 데이터가 굉장히 적음을 의미하기 때문이다. Nearest Neighbour Regression의 경우도 같은 단점을 지니고 있다.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://bkshin.tistory.com/

Unsupervised Learning

The challenge

이전 챕터들에서 supervised Learning 에 관해서 여러가지들을 배웠다. 만약 이진 결과값을 데이터로 부터 도출하여 추측하여야 한다면, 로지스틱, LDA, classification Trees 등을 이용하여 값을 도출하고, 이 결과값에 대하여 어떻게 접근해야 할지에 대한 명료한 지식들을 배웠다 (CV, validaton…)

반면에 unsupervised learning 의 경우 조금더 어려운데 이는 대부분의 실험들이 주관적이고, 분석 (예측)과 같은 간단한 목표를 가지고 있지 않기 때문이다. 대신 unsupervised learning은 exploratory data analysis 에 대한 부분으로 행해진다. 또한 결과값을 도출하는데도 어려움이 있을수 밖에 없는 이유가 이 모델이 맞는지에 대해 테스트 할 수 있는지에 대한 방식이 존재하지 않기 때문이다 (예를 들어 예측하는데에 대해 예측할 값이 존재하지 않는다던가)

PCA

correlated variables가 많은 데이터를 마주 하였을때 principle component (PC)를 이용하여 더 적은 변수들로 대부분의 variability를 summarize 하여 설명할 수 있게 해준다. 챕터 6에서 이야기 하였듯, PC directions는 본래의 데이터에서 highly varaibla한 방향을 보여줌과 동시에 데이터 클라우드에 대해 가장 가까운 선과 부분 공간을 보여준다.

PCR을 사용하기 위해서, 우리는 PC를 예측 변수로 사용한다. 이 PC를 이용해 supervised 한 방법이 (PLS)

PCA는 또한 데이터 비율어화에 대한 도구로써 사용되고 한다

Principal Component란 무엇인가

2차원의 scatter plot을 이용하여 데이터간의 관계를 보통 확인하는데 p=10일 경우, 그려지는 그래프만 45개에 달한다. 또한 각각의 그래프 또한 딱히 중요하지는 않을텐데 이는 각각의 그래프가 나타내는것이 총 데이터에서 일부분에 지나지 않기 때문이다. 즉 우리가 2차원의 그래프를 그릴때, 해당 변수가 데이터에 대해 가장 영양가 있는 (informative) 상황이라면 우리는 큰 데이터를 더 낮은 차원의 공간에서 관찰할 수 있게 되는것이다. (즉 데이터에 대해 가장 잘 나타내는 변수만 관찰하면 파악하기 쉬우니까)

PCA provides a tool to do just this. It finds a low-dimensional representation of a data set that contains as much as possible of the variation. 여러개의 변수중에 흥미로운 변수 (차원들)을 파악하려고 노력하는데 이는 관련 변수의 observations가 각 차원에서 얼마나 vary하는가를 기준으로 한다.

계수로 인한 분산이 무한이 커지는것을 막기위해 합을 1로 제한한다.

기존의 데이터셋에 공분산 행렬을 생성하고 (괄호 안), 고유의 Vector와 값을 계산 (대괄호). 그런 다음에 고유 값이 큰 순서대로 정렬 후 변환해야할 차원의 수 만큼 고유 값을 정한 뒤. 고유 Vector에 투영하여 차원을 축소한다.

머신러닝 - 9. 차원 축소와 PCA (Principal Components Analysis)

variance가 maxmized 될때 데이터 클라우드에 가장 가까운 이유가 이 때문. variance가 maxmized 되어야 information loss를 최소화 할 수 있다.

1st Principal Component (PC1) 은 주어진 변수들 중에서 데이터를 강 잘 설명하는 성분이다. 만약 PC1의 기울기가 0.25라면, feature 1 increases 4 then feature 2 increases 1 의 선형 결합이 (Linear Combinaito) 해당 데이터를 가장 잘 설명하는 요소라는 의미가 된다.

위의 그래프에서 PC1은 Rape Assault Murder에 가중치를 더 부여하고, PC2는 UrbanPop에 더 가중치를 주는것을 볼 수 있다. 따라서 UrbanPop은 변수들이 설명하고자 하는 도시화에 대해 roughly corresponding 한다고 볼 수 있다. 전체적으로, 범죄와 관련된 변수들이 서로 가까이 있으며, 인구수는 이들과 동떨어져있다. 이는 범죄와 관련된 변수들은 서로 correlated되어 있음을 의미한다.

위의 그래프로부터 다음과 같이 해석될 수 있다. 버지니아와 인디애나 같은 주들은 평균치에 가까운 범죄율과 도시화를 가지고 있고, 캘리포니아는 높은 범죄율과 높은 도시율을 가지고 있다고 본다. 이에 비해 하와이는 낮은 범죄율을 가지면서 높은 도시율을 가졌다.

Another Interpretation of Principal Components

위 섹션에서는 PCA를 이용한 시각화 그래프에 대해 variance 최대화에 초점을 맞추었는데. PC1의 로딩 벡터는 또다른 특별한 특징을 가지고 있다: p 차원의 공간에서 n개의 관측점에 대해 가장 가까운 선이라는것. 이 해석이 말하고자 하는것은 매우 분명한데 이는 “모든 데이터에 대해 가장 가깝게 그려진 일 차원 데이터를 찾는데, 이는 이 선이 모든 데이터에 대해 좋은 요약을 해줄것이기 때문” 물론 반드시 일 차원 데이터를 찾는것은 아니다 (적을수록 좋다는것)

90개의 샘플에 대하여 왼쪽은 삼차원, 오른쪽은 이차원으로 나타낸것이다. 즉 오른쪽에 대해 한 차원을 더 포함한 (third PC) 상태.

More on PCA

변수들 스케일링 하기.

위에서 우리는 PCA를 하기전에 변수들의 평균이 0이 되도록 센터링 시켜야 한다고 하였다. 이에 더불어서 우리가 PCA를 통해 도출한 결과값은 변수들이 각각 얼마나 스케일 되었는지에 대하여 dependant 하다. 이는 다른 supervised & unsupervised 와 차이점으로 존재한다 (다른 방법들은 스케일링으로 인한 결과값이 변하지 않는다).

왼쪽의 경우 위와 같이 SD의 총합이 1이 되도록 scaling 한 상태. 오른쪽에서 Assault가 PC1에서 가장 큰 로딩을 가지고 있는데 이는 다른 변수들에 비해 가장 높은 분산을 가지고 있기때문이다. 또한 각 변수들의 unit 또한 각기 다르기 때문에 (100명당 하나, 1000명당 하나, 돈의 경우 1000달러 등등) 그냥 기본적으로 SD를 1로 설정하는 방식이 추천된다.

These four variables have variance 18.97, 87.73, 6945.16, and 209.5, respectively. Consequently, if we perform PCA on the unscaled variables, then the first principal component loading vector will have a very large loading for Assault , since that variable has by far the highest variance.

만약, 모든 변수들이 같은 unit으로 측정되었다면, SD를 1로 하지 않는게 좋다.

Uniqueness of the Principal Components

Each PC loading vector는 고유하다. 이 로딩 벡터의 사인 (플마)는 바뀔지 언정 값 자체는 어느 소프트웨어 패키지에서 실행하던지 같다. 또한 이 사인의 변동또한 의미가 없는것이 결국 방향을 이용하여 분석하기 때문. 따라서 loading vector, and score vector 가 동시에 사인이 바뀌는 이상 최종 결론에는 문제가 없다. (하나만 바뀌고 그러면 안됨)

Proportion of Variance Explained

위와 같은 방식으로 각각의 PC가 얼마만큼의 분산을 설명하는지에 대하여 알 수 있지만, 어느선에서 얼마정도의 PC가 필요한가? 에 대한 사항은 특별히 정해진게 없다. scree plot (각각의 PC의 분산 설명도 그래프) 을 이용하여 elbow 를 이용하여 정할수도 있긴 하다. 현실적으로, 혹은 실증적으로는, 우리는 첫 몇몇의 PC를 시각화해서 특이한 패턴이 있는지 확인 하는 식으로 결정한다. 당연하게도, 이러한 방식의 접근은 매우 주관적이며 이로 인해 우리는 PCA는 exploratory data analysis를 위한 시각화 도구로 사용하는 이유중 하나다.

물론 PCA를 supervised에 사용한다면, CV와 같은 방법을 이용하여 score vectors 를 regresisson 튜닝 패러미터로 사용된다면, 몇개의 PC가 사용되어야 하는지 알 수 있다 (왜냐면 이걸 지금 어디에 쓰는지 우리가 분명하게 알고있으니까)

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. [ISL] 6장 -Lasso, Ridge, PCR이해하기

Dimension Reduction Methods

앞서 공부했던 방법들은 몇 변수만 선택하거나, 계수들을 0으로 줄이는 방법과 같은 variance를 줄이기 위함이었다. 차원축소 방법은 변수 자체를 변환하여 분산을 줄이는 방식이다

기존 p개의 변수들에서 m의 변수들을 이용한 Least Square 를 이용한 적합을 하는것 (M<P)

이처럼 제약이 있는 상태에서 계수를 정하면 bisa가 생기나, 이로 인해 variance가 눈에 띄게 감소 되므로 결과적으로는 더 좋은 모델들이 만들어지는것이다.

Principle Components Regression

Principal Components Analysis (PCA)

n*p의 크기를 가지고 있는 x를 줄이기 위해 데이터들의 변동(분산)을 가장 잘 나타낼수 있는 first principal component direction을 찾는다 (이 선이 분산의 크기가 가장 크다)

이 계산 과정에서 데이터 중심에 축을 두고자 centering을 하게 되는데, 이 방식은 분산에 영향을 미치지 않아 결과는 같게 된다.

물론 분산의 무한함을 방지하기 위해 두 계수의 제곱합은 1과 같다라는 제약을 걸어 두었다

이렇게 만들어진 Z1 = principal component score라고 불린다.

왼쪽의 초록선은 데이터가 가장 큰 분산을 가짐과 동시에, 모든 n개의 관측값에 가장 가까운 선이기도 하다 (즉 수직 점선들의 거리가 가장 짧게). 파란점은 (pop,ad) 의 평균 값을 의미한다. 오른쪽의 그림은 2차원으로 표현된 왼쪽 그림은 회전시켜서 1st PC의 방향이 x축과 같아지게 만들은것. 이 1st PC의 값은 결국 저 파란점과의 거리를 의미하며, 음수이면 두 평균값보다 낮고, 양수일수록 두 평균값보다 높은것이라고 해석을 할 수 있는것.

위의 왼쪽 그래프에서 볼 수 있듯, 두 변수는 선형관계를 가지고 있는데, 이를 파악하여 정보를 압축한 1st PC는 각각의 변수에 대해 강력한 선형 관계를 보여준다.

p개의 변수는 곧 최대 p개의 다른 component를 만들 수 있음을 의미하는데,

2nd PC의 경우

1. 1st PC와 uncorrelated
2. 1st PC가 미처 설명하지 못한 부분

에 대해 설명 할 수 있는 방향, 즉 1st PC의 제약 하에 가장 분산이 큰 방향으로 linear combination이 결정된다. 위 오른쪽 그림에서 수직선들에 대해 2nd PC가 사용된것이

왼쪽 그림에서 이와 같이 표현될수 있다. 초록색이 첫번째, 파랑이 두번째 PC

이 두 PC는 (두 선은) 직교 (90도)를 유지하는데, 이는 두 관계가 zero correlation임을 의미한다. 현재는 변수가 2개여서 2개만 있지만, 더 높은 다차원은 여러 방향의 선으로 분산이 가장 높은 방향의 선을 긋는다.

저 위의 오른쪽 그림에서 보이듯, 1st 에 비해 2nd의 값의 수치가 훨씬 적다는 것을 확인 가능하다 (1st는 -25 ~ 20, 2nd는 -10~10). 지금은 변수가 두개여서 불가능하지만, 여러 변수가 있는 상황에서 이와 같은 형태는 차원을 축소 할 수 있다는 것을 의미한다 (1st가 대부분의 정보를 포함하니까 굳이 2nd까지 가지고 있을 의미가 없지). 따라서 차원을 축소함에 따라 이전 compnent에 비해 uncorrelate하면서도 variance가 가장 큰 방향으로 component를 결정 가능하다.

Principal Components Regression Approach (PCR)

PCR은 PCA를 통해 만들어진 M개의 예측변수들을 통해 Least Square적합을 하는것.

“p개의 변수를 가장 큰 variation으로 나타낼수 있는 direction 은 Y와 연관이 있을것이다” 라는 가정하에 이루어지는 분석이므로, 이 가정이 항상 참일수는 없으나 대게의 경우 좋은 적합을 보여준다. 또한 가정이 맞을 경우, 전의 p개의 변수보다 더 적은 m개의 변수를 사용하므로 overfitting을 완화할 수 있다. (n이 p보다 크지 않다면 - 데이터가 변수갯수보다 일정이상 크지 않다면 least square의 변동성이 큰 결과를 내고 overfitting이 커짐을 다시 기억하자)

저번 블로그에서 마지막에 나왔던 데이터에 관한 PCR결과이다. 왼쪽의 경우 45개의 변수중 45개 모두가 유의미한 데이터인 경우, 오른쪽의 경우 2개의 변수만 중요할 때이다. 더 많은 component를 사용할 수록 bias decreases, but variance increases

45개의 component 사용한 값은 단순히 Leaner Square에 모든 변수들을 사용한 것과 같은 값을 보여준다. 왼쪽의 경우 15개 정도의 component에서 성능 증가를 보인경우에 비해 오른쪽은 훨씬 더 많은 component를 가져야 TEST MSE가 낮아졌다.

이는 PCR의 가정, 몇몇의 component로 데이터의 분산을 잘 나타낼 수 있고 Y의 관계가 있을것이다, 이 충족될때 큰 성능을 발휘하기 때문이다.

PCR은 변수 선택법이 아니고, 모든 기존의 p개의 변수가 선형결합으로 포함된 변수이다. 이는 PCR이 Ridge의 continuous version이라고 할 수 있다.

Partial Least Squares (PLS)

앞의 PCA는 unsupervised 방식으로 Y값을 전혀 고려하지 않았다. 이 방식은 PCR의 단점을 곧 의미하는데 (PCA를 이용했으니까 PCR이) 예측 변수들의 관계를 가장 잘 설명하는 방향이, 반응변수 (Y)를 설명하는 예측 변수들의 관계를 가장 잘 설명하는 방향이 아닐수도 있다는것.

PLS는 이 방식을 보완했는데, 같은 방식이지만 M개의 변수들을 supervised해서 만들어 내는데, 이로 인해 반응변수와 관계된 변수들의 관계를 더 잘 나타낼수 있는것.

PCR과 마찬가지로, PLS역시 변수들을 표준화한 후 계산해야하고, 몇개의 direction을 만들것인지는 cross-validation을 통해 알아본다. 그러나 실제에선 PLS는 supervised라는 점에서 bias는 줄여주지만 그에 상응하여 variance가 높아지기에 PCR이나 Ridge만큼의 성능을 보이지 못하는 경우가 많다.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Why Not Least Square?

OLS 는 오차의 평균이 0, 오차의 분산이 등분산 (모두 비슷함), 그리고 오차가 서로 관계가 없는 선형 모델중에서 최적이다. 또한 분포가 정규분포일 경우, OLS estimator 는 Maximum Likelihodd estimator 와 같은 결과를 낸다.

OLS는 unbiased 한 대신 variance하고, 이로 인해 데이터에 따라 변동차이가 크다. 하지만 다음과 같은 이유로 OLS를 대신하는 대체 방법들이 존재한다.

1. 예측정확도:
   • OLS는 가정된 분포가 어느정도 맞고, 변수의 개수 p보다 자료의 개수 n이 훨씬 많을때 좋다.
   • 만약 n이 p 보다 (보통 3배) 많지 않다면, OLS는 큰 변동성 (variance)를 가지게 되고, 이로 인해 새로운 자료에 대해 예측을 잘 못하는 overfitting 이 나타난다. variance = p * (SD/N) 이므로, p가 클 수록 증가한다.
   • 만약 n이 p 보다 적으면, OLS는 variance가 무한인 사용 불가능한 방법이다. 이 이유는 matrix 연산에서 full rank인 matrix만 가능한데, n<p는 비가역행 행렬 (non full rank) 가 된다.
2. 해석력:
   • OLS는 Y에 전혀 관계가 없어도 0으로 제외할 수 있는 능력이 없다. 즉 중요한 변수를 선택하고 무쓸모한 변수를 제외하는 능력이 없음. 그래서 5장에서 사용한 방법들이 존재하는것.

Options?

1. Subset selection: 유의미한 변수를 골라내고 OLS 하는것
2. Shrinkage: 모든 변수들을 이용하여 저합한다. 계수들인 OLS에 비해 0으로 가려고 하는 경향이 있다. 자동적인 변수 선택도 가능하게 한다.
3. Dimension Reduction: p개의 차원 (변수)에서, m의 차원 (변수)로 projection 후 OLS 하는 방법.

Subset Selection

Best Subset selection

모든 경우의 수를 써보고 최고를 찾는법. 하지만 p가 클수록 ovrefitting 된 모델을 고를 확률도 늘어남.

1. 변수 p개 중에서 0 ≤ k ≤ p 인 모델 모든것을 계산 하는 방법
2. 각 k개의 모델들중 R^2 이 가장 높은거 선택 (변수 수가 같으니 간단하게 찾기 가능)
3. 뽑힌 모델들중 최고를 뽑는것. 변수의 갯수가 달라 R^2은 이제 못쓰고 CV-error, AIC, BIC, Radj 등을 쓴다.

다시 말하지만 변수의 수가 많을 수록 설명력이 당연히 강해지고, 이로 인해 low training error값인 R^2이 좋게 나올수 밖에 없다. 하지만 우리의 목표는 테스트 에러지, 트레이닝 에러가 아니다.

이 방법은 계산양이 많다는 단점이 있다.

Stepwise Selection

Best Subset selection의 단점인 계산양과 잘못된 모델 선택의 대안으로 사용 가능한 방법이다.

• Forward Selection: 보수적인 모델 (변수가 최소화된) 을 선택함
• backward selection: 변수가 많이 들어간 모델을 선택함
• mixed selection: 제일 best subset selection과 비슷한 모델을 찾아줌

이 세가지 방법들은 best 모델을 찾는것이 보장되어 있지는 않다. 세세하게 다른 차이점이 존재한다.

Choos Optimal Model

test error를 최소화 하기 위한 방법이 두가지 가 존재한다.

1. Overfitting 을 고려한 수학적 보정을 통안 test error의 간접 추정
2. Traninig est중 몇개를 빼서 하는 직접 추정 (5장에서 배운것들)

간정 추정들로는 CV-error (C_p), AIC, BIC, adjusted R^2 이 존재한다.

위에서 RSS = SSE_r (reduced model SSE)를 뜻한다.

Validation and Cross-Validation

예전에는 컴퓨터의 계산 능력으로 위의 방법들을 선호 했지만, 이제는 CV를 더 선호한다.

위의 방법과 CV는 몇개의 그룹으로 잘렸는지, 혹은 데이터가 어떻게 나뉘어졌는지에 따라 변동될 수 있어, 선택된 변수 숫자가 최적의 모델이 아닐수 있다. 이를 해결하기 위해서 one-standard-error rule을 적용한다.

Test MSE 의 SD의 SE 를 구한뒤, 최소 Test MSE에서 SE만큼 떨어진 모델들을 고려하는것이다. 즉 최소 Test MSE 의 갯수가 4이면, 앞뒤로 1개씩 더 총 3개를 고려하는것이다.

Shrinkage Methods

모든 변수로 적합하되, 계수들을 0으로 constrain 혹은 regularize하는 방법이다. 이 방법은 추정된 계수들의 (hat values)의 variance를 대폭 줄여준다는 장점이 있다.

Ridge Regression

기존의 RSS + 모든 계수 합의 제곱 * 람다 의 값을 최소화 하는 식이다. 따라서 계수들이 점점 줄어든다.

이 방식으로 데이터 적합성을 올리는 동시에 계수들을 0 으로 가게한다. 다만 이 계수는 intecept 값을 포함하지 않는다.

람다 값이 커질수록 shrinkage 효과에 더 비중을 두는 식이다. 이 람다 값은 CV를 통해 결정하며, 0일때는 기존의 OLS와 똑같다.

주의해야 하는점은 이 추정되는 계수는 람다에만 영향을 받는게 아니라 변수들의 스케일링에도 영향을 받는다. (애초에 그 계수가 어느 스케일링을 기준으로 만들어진거니까) 따라서 표준화 작업을 해주고 시작을 하게되면, 모든 변수들의 표준편차는 1이 되며, 이로 인해 Ridge regression이 스케일링에 영향을 받지 않는다.

Why Ridge?

람다가 증가함에 따라 flexibility는 감소하고 Variance가 감소하고 Bias는 증가하게 된다

즉 Bias Variance Trade off 에 있는것이다.

Bias는 람다값의 변화에 따라 조금씩 바뀌지만, Variance의 경우 람다가 증가함에 따라 큰폭으로 감소한다. 이는 람다라는 제약에 따라 계수들이 shrinkage 하면서 변동이 크지 않는 모델이 나온다는 의미이다. (점점 람다 값에 미미해져가는거).

선형에 가까울때

• OLS: unbias 하지만 variance가 높고, 이는 데이터의 변동에 계수가 크게 변동한다는 의미이다. 또한 p>n 일때 OLS는 유일한 해가 없다 즉 모델을 만들때마다 값이 다 다르게 나오는거
• Ridge: 약간의 bias 손해소 varaince 를 크게 줄인다. p>n 일때 덜 flexible한 적합을 통해 소수의 데이터 특성에 국한되지 않는 모델을 만드는것. 또한 람다 계산은 한번만 하면돼서 best subset selection에 비해 계산이 간편한 장점이 있다.

Lasso

Ridge의 단점

Ridge Regression의 방식은 예측과 관련해서는 아무런 문제가 없지만, 해석측면에서 약점을 가지고 있는다. 만약 해석의 경우 1,2,3 변수만을 통해 하고 싶다고 하자. 다만 Ridge는 모든 변수로 적합을 해야만 하고, 나머지 계수가 0이 아니다 (0에 가깝다) 즉 1,2,3 변수만을 통한 해석이 쉽지 않은것.

적당한 람다 값으로, 몇몇 계수를 정확하게 0으로 만들어서 ridge 보다 더 강령한 해석이 가능한것 (나머지 불필요한 계수들이 모델에서 사라진것이니까). 따라서 Ridge보다 더 적은 변수들을 포함하기에 sparse model 이라고 한다.

Ridge와 다르게 위에서 rating 계수만 끝까지 남아 있다가 사라진다. 즉 람다 값이 올라감에 따라 변수들이 차례차례 0이 되어 버리므로, 원하는 계수들만 가지고 있는 람다값의 선택이 가능한것. Ridge 는 꾸준히 같이 함께 줄어든다 (마치 비율처럼).

다른 식

위의 Ridge, Lasso, best subset selection 은 다른 식으로 표현 가능한데, 식들을 살펴보면

Lasso and Ridge는 Best subset selection을 실현 가능한 형태로 대체한 식임을 알 수 있다 (즉 계산의 부담을 덜은점). 특히 Lasso는 명확하게 변수를 없앤다는점에서 Best subset과 더 유사하다.

Lasso 변수 선택 성질

빨간선이 RSS, hat value는 OLS점이다. 만약 s 가 충분히 커서 hat value를 포함하면, 이는 OLS와 같은 값을 가지게 된다. 즉 hat value는 해당 제약범위 (초록색)과 가장 작은 RSS와 만나는 지점일 것이다.

Lasso는 사각형의 모양이라, 다른 계수가 0인 지점에서 쉽게 교점이 생긴다. b2 축에서 교점이 생겼으므로 b1 = 0 이 된다. 하지만 Ridge의 원 모양은, 한 계수가 정확히 0인 교점이 생기기 힘들다. 즉 한놈만 선에 닿는 일이 벌어지기 힘들다. 왜냐면 공평하게 퍼지니까.

Lasso and Ridge 차이점

해석력은 Lasso가 변수들을 완전히 제외시킴으로써 더 쎈거는 이제 알게 되었다.

오른쪽 그림에서 두 방법 모두 bias는 비슷하지만 ridge의 variance가 약간 더 낮아서 Test MSE가 Lasso 에 비해 더 낮다. 하지만 이 경우는 모든 데이터가 Y값과 관련이 있는 (correlated)한 데이터 였다. 이에 따라 몇 계수들을 제외한 Lasso 가 불리하다.

위 처럼 만약 2개의 변수만이 유리하다면, Lasso 가 Test MSE를 더 낮은 값을 가진다. 즉 두 방법의 성능은 데이터 상황에 따라 다른것이다. 이를 알기 위해 CV 방법을 사용한다.

람다값 정하는 방법

몇몇 람다값을 선정해서 CV해보고 이중 가장 적은 CV-error를 가진 값을 선정하고, 이 계산에 쓰인 데이터를 원래 총 데이터에서 빼서, 새로운 데이터에 뽑은 람다 값을 이용하는것이다.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Resampling

Extract sample from training data set, and apply series of models.

Application of several models will allow users to estimate which “region” will our models be when the data gets changed.

Cross-Validation

Test error and training error are different.

• Lowering the test error (data that was not given) is the goal.
• Training error is the error in the given data that can be underesitimated due to overfitting.

There are two ways of esitimating test error (often future prediction case)

1. Indirectly infer test error by mathematical edition on the training data set (AIC, BIC).
2. Hold out some training data to directily infer test error (Cross-Validation).

The vaildation set approach

Hold out half of training set randomly — picked data is called vaildation set.

• 반을 자르기 때문에 어떻게 잘리느냐에 따라 모델 변동과 test MSE 도 심하게 변함
• Use remainder training set to get error rate (ususally MSE) about vaildation set and infer test error rate.

Degree of polynomial 이 에러를 줄이는데 도움이 안됨을 알 수 있다.

1. 어떻게 잘렸는지에 따라 test MSE와 degree 또한 확연하게 달라진다
2. 반을 잘랐기 때문에 추정 성능 또한 감소한다 - 반으로 적합하다고 모델을 정의 하면, 전체 자료를 적합했을 때는 test MSE가 크게 나올수 밖에 없다 (overestimate 한거니까). 반으로 전체를 예상할수 있다고 한것

Leave-one-cut Cross Validation (LOOCV)

한개의 자료를 빼고 이 자료에 대한 error rate 을 계산하는데, 이 계산을 모든 자료에 반복한다.

Training MSE is unbiased to Test MSE but has huge variance. Random error 를 포함하고 있어 이로 인해 분산이 생기는것. 이 분산들을 보완해주는게 validation 이다. validation으로 분산을 줄이지만, 약간의 bias가 생긴다. 이 약간의 편향된 모델들을 평균냄으로써 분산이 줄어드는것

1. 데이터 반을 가지고 하는것에 비해, test MSE에 대한 training data가 거의 정확한 추정이 가능하다. 이는 overestimate 하지 않으며 bias가 적음을 의미한다
2. Validation set approach 와 다르게 항상 같은 결과가 나온다.

K-fold Cross-Validation

가장 대중적으로 test error rate 구할때 사용하는 방법이다. 최선의 모델이나, 최종 선택된 모델에 관한 테스트 에러에 대해 이해하는데 사용된다.

Validation set approach 는 너무 단순하고 LOOCV는 손이 너무 간다 (하나하나 적합해야 하니까). 이 중간지점이 k-fold CV. k 그룹으로 랜덤하게 데이터를 나눈다. 한 그룹을 뺴고 적합해 MSE 구하는것을 k번 반복한다 (LOOCV 처럼). 이후 K로 평균을 낸다.

k = n 일경우 LOOCV와 같은식이다.k-fold CV는 LOOCV에 비해 더 간결하고 빠르게 계산을 함에도 불구하고 성응에서 큰 차이를 보이지 않는다 (좋은쪽으로). 즉 LOOCV의 장점들을 다 가지고 있다. 또한 bias-variance trade off에서 LOOCV보다 더 강점을 가지고 있다 (다음 항목 참조)

Bias-Variance Trade off for k-fold CV

위 식에서 알 수 있듯 test MSE는 bias 만으로 결정 되는것이 아니다. Variance의 관점에서 (위에 서술하였듯) LOOCV 보다 k-fold CV가 더 좋다.

• LOOCV는 낮은 bias와 높은 variance를 가지고 있는데 이는 적합시의 데이터 n-1개중 n-2가 동일한 데이터 (두개의 적합에서 2개를 제외한 나머지 데이터는 재사용된것들) 따라서 재사용을 많이한 n개의 모델들는 highly correlated 되었기 때문이다. highly correlated —> higher variance (overfitting과 비슷한 개념)
• 이로 인하여 덜 겹치는 k-fold CV가 더 낮은 분산을 갖는것이다

CV on Classification Problems

식이 조금 달라졌다. 이전까지의 계산은 데이터 수에 대한 양적 변수를 가정한 CV였고 위의 식은 질적 변수에 대한 식이다 (질적 테스트는 error rate를 의미한다)

검은색 선이 10-fold CV인데 파란색인 training error에 비해 테스트 에러를 잘 잡아주고 잇는 모습이다. 저 테스트 에러는 진짜 테스트 에러로 (시뮬레이션 데이터를 이용한) 실 상황에서는 구하지 못하는 경우가 많은 선. 따라서 위 그래프는 진짜 에러 비율에 대해 k-fold CV가 어느정도로 잘 잡아주는지 보여주는 것.

Bootstrap

실제로 계산하기 어려운 uncertainty 들을 계산하는데 쓰이는 강력한 기법이다. 선형희귀의 계수 분산의 경우 표준편차 정도는 구할 수 있지만 이에 대한 정확한 통계량은 구할 수 없는데, bootstrap은 이를 가능케 한다. 또한 이 방법은 분포를 미리 가정하지 않은 (실상황처럼) 상태에서 사용 할 수 있기 때문에 더 강력한것.

밑의 식은 a, 1-a를 각 두 회사에 비율 투자할때, 분산을 (risk) 최소화 할 수 있는 비율을 찾는식이다.

위와 같은식을 사용 할 수 있는 이유는 아래와 같이 가지고 있는 데이터들을 복원추출 하여 새로운 샘플들을 계속 만들어 내기 때문. 밑의 식을 반복하여 큰 수인 n 개의 샘플들을 만들어 이에 대한 추정량 hat(a)가 생기는것.

위의 식을 이용하며 추정량에 대한 standard error 또한 구할수 있게 된다.

노란색이 모든 자료들을 가지고 반복 추출해서 구한값, 파랑색이 bootstrap으로 하나의 data set만으로 반복추출해서 얻은 결과이다. 매우 비슷함을 알 수 있는데, bootstrap이 적은 data set으로 구하기 힘든 통계량의 특성까지고 구사 한다는것을 알 수 있다.

Bootstrap for Prediction Error?

bootstrap 샘플의 경우 원래 데이터 들과 많이 겹치게 되는데, 이로 인해 true prediction error 을 많이 underestimate 하게 된다. 마찬가지로 원래 데이터들을 훈련 샘플로 쓰고 bootstrap의 데이터들을 vaildation 에 쓰게 되면 안 좋은 (쓰레기 같은) 값이 나온다.

이에 대한 데이터 셋 겹침을 구할수 있으나, 매우 복잡해지고 이로 인해 결국 CV가 prediction error를 예상하는데 더 나은 방식이 된다.

정리하자면 Test error rate을 구하는데는 bootstrap. Prediction error을 구하는데는 CV.

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Why Not Linear Regression?

There is no natural way to convert a qualitative response varaible with more than two levels into a quantitative response that is ready for linear regression. Therefore, better use classification.

Logistict Regression

It models the probability that Y belongs to a particular category (All probabilities lie between 0 and 1).

The function will always produce S-shaped curve, hence regardless of X, we will obtain a sensible prediction.

The fact that it is not a straight line between p(X) and X, and the rate of change of p(X) per unit change in X depends on the value of X, can be seen by the line.

Estimating the Regression Coefficients

In case of Logistic Regression, MLE is suitable than Least Square to estimate coefficinets in case of non-linear models. Hence, Maximum Likelihood takes parameter b0 and b1 that makes below Likelihood function max.

z-stat : hat(b1)/SE(hat(b1)) —> large (absolute) value indicates evidence against the null hypothesis: b1 = 0 in p(x) although still use p for hypothesis test.

For multiple predictors more than two, Linear Discriminant Analysis is better.

Usually good under parameter ≤ 2

Linear Discriminant Analysis

Esitmation through the distribution of Xs. P(X|Y) through Bayes.

• When the classes are well-separated, the parameter estimates for the logistic regression model are unstable; LDA does not have this.
• If n is small and predictors X approx norms in distribution, LDA is more stable.
• LDA is more popular when having more than two response.

Bayes’s Theorem for Classification.

To classify into one of K classes (K ≥ 2); meaning Y can take K possible distinct and unordered values.

Posterior Likelihood = Prior Likelihood * density function/ …

If we can estimate Posterior Likelihood corrcetly, ideal classifcation that has low error con be made.

Esitmating posterior likelihood is hard, so need to assume particular distribution for density function.

LDA for p = 1

Assumption: Normal/Gaussian Distribution; each different distribution exists among K (num of class) with its corresponding mean and shared variance.

Use log for above equation and remove duplicated term that not changed to certain k —> giving you the largest class k! Since log is one to one func —> no info loss.

To implement LDA

1. Estimating the parameters
2. Compute the decision boundary that results from assigning an observation to the class for which Var_k is the largest (above figure, bottom).
3. Left, right of this dotted line represents each classes.

Comparing Bayes Error Rate and LDA error rate to see how the model does.

최종 정리하자면, LDA는 ‘ fk(x)=P(X=x|Y=k) 에 대한 정규 가정과 각 클래스마다 다른 평균, 동일한 분산’을 가정하여 Bayes classifier의 확률을 추정하는 방법이다. 뒷장에서 ‘등분산’에 대한 가정을 떼어내는(즉 클래스마다 σ2k를 가질 수 있게 하는) 방법을 배울 것이다.

출처:

[ISL] 4장 - 분류(로지스틱, LDA, QDA) 이해하기

LDA for p > 1

Assumption: Each multivariate Gaussian —> each class has diff mean, and still shares the same variance.

Multivariate Gaussian: each variable follow its Gaussian Distrib, and each variable pair has correlation —> can be seen as mulit-dimensional Gaussian Distrib.

• Left: Two predictors are not correlated; meaning Xs’ variacne are the same, while correlation = 0.
• Use Bayes Equation gives the second equation above; choosing the largest K.
• Since it is still a linear to X, it is LDA.

Problem of Null Classifier

LDA has low on training error rate but

1. It will usually lower than test error rates; meaning it may perform worse to predict a new data. Because specifically adjusted the parametrs of the model to do well on the training data. The higher ratio of parameters p to number of samples n, the more expect overfitting.
2. The trivial null classifier will achieve an error rate that is only a bit higher than the LDA training set error rate.

Confusion Matrix can identify the binary classifier error (putting into different category).

Sensitivity : if the targeted class well measured.

Specificty: if the non-targeted class well measured.

Why does LDA do such a poor job of classifying the customers who default? In other words, why does it have such a low sensitivity?

• LDA is trying to approximate the Bayes classifier, which has the low est total error rate out of all classifiers (if the Gaussian model is correct).
• The Bayes classifier will yield the smallest possible total number of misclassified observations, irrespective of which class the errors come from.
• Meaning if classify as non-default will be likely correct in this case, the model be considerate at classify the data as default.
• In this case, using lower threshold could be a solution.

Recall: TP/P - 재현율 (진짜 애들중 몇명) Precision: TP/P* - 정확률 (잡은 애들중 진짜가 몇명).

Quadratic Discriminant Analysis

Unlike LDA, each class has its own covariance matrix in QDA. Still use multivariate nomal distrib and use Bayes theorem.

This function is not linear to X, hence called QDA —> therefore decision boundary is non-linear as well.

• For LDA, cov matrix = p(p+1)/2 hence it is less flexible and low variance model. However it will have high bias if it is not nomally distributed (which is in most real cases). If less variance is more important because of small training data, use LDA.
• For QDA, cov matrix = Kp(p+1)/2. If large training data (so less concern with variance) exists, or covariance seems unrealistic (not normally distributed) use QDA.

Comparison of Classification Methods.

LDA and Logit

• Both creates decision boundary although use diff calculations.
• If it is close to normal distribution, LDA is better. If not, Logit.

KNN

• If decision bondary is non-linear, it would be good.
• It will not be good for intepretation for which variable played an important rule —> Since the purpose of this method is to analyze the data status.

QDA

• KNN+LDA+Logit characteristics.
• Less flexible than KNN, but decision boundary is Non-linear
• Hence it is more flexible than LDA.
• Due to the assumption of distribution, it will more fit in small data unlike KNN. (Ofc needs more data than LDA as it has more parameters).

Case Experiment:

1. Diff mean, Uncorrelated, Normal Distribution
   • LDA did the best due to the distribution.
   • KNN and QDA are too flexible for distribution so bias (strength it has) did not show off much, and has higher variance —> did not do well.
   • Logit is slightly worse than LDA since the boundary decision is linear.
2. Diff mean, correlation : -0.5, Normal Distribution
   • It means multivariate normal distribution
   • Same as 1.
3. t-distribution
   • Since assumption of LDA is violated, Logit > LDA > KNN, QDA
   • It is because it is still similar to Normal Distribution.
4. First class : 0.5 corr with normal dist, Second class: -0.5 corr with normal dist.
   • Satisfies QDA assumption, hence QDA was the best.
5. 2-Polynomial Decision boundary
   • QDA then KNN-cv
6. More non linear than 5th one
   • KNN-cv > QDA > LDA,Logit > KNN-1
   • It states k does matter as 1 is too flexible.

출처: https://godongyoung.github.io/머신러닝/2018/01/23/ISL-Classification_ch4.html

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Linear Regerssion is uesful tool for predicting a quantitative response. It is a good jumping-off point for newer approaches.

SLR

• It assumes there is a approximately a linear relationship between X and Y.
• hat denote the estimated value for an unknown parameter or coefficient or to denote the predicted value of the response.

Estimating the Coefficients

• Wants to find parameter and coefficient as close as possible → use Least Squares

Assessing the accruacy od the Coeff Ests.

Population Regression Line: Generally not known.

• best linear approximation to the true relationship between X and Y.
• Each regression line may differ from this as the models are based on a separate random set of observations.

The purpose of using least square is to estimate caharacteristics of a large population.

If we estimate certain parameter based on a particular data set, it may overestimate or underestimate. However, observing huge amount of data and average will give us the exact value of it. Hence, treat the estimates as unbiased (such as hat values).

Stadarad Errors

• tells us the average amount that this estimate hat(mean) differs from the actual value of mean.
• can be used to conduct the confidence interval.
• can be used to perform hypothesis tests on the coeff.
  • t = hat(b1) - 0 / SE(hat b1)
  • if SE(hat b1) is small, it means the strong enough to reject null hypothesis
  • t measures the num of SD that hat(b1) is away from 0.
  • if no relationship, will have t-distrib with n-2 degrees of freedom.

p-value: indicates the unlikeness to observe the association between predictor and the response. Therefore, small p implies the associtaion.

The accuracy of the model

After we performs the hypothesis tests, want to quantify the extent to which the model fits the data by using: residual SE, and R^2 statistic.

1. Residual Standard Error (RSE):

   

   • is an estimate of the standard deviation of error.
   • is the average amount that the response will deviate from the true regression line.
   • measure of lack of fit —> Small RES : well fit of data.

2. R squared: takes the form of proportion.

   

   • TSS measures the total variance in the Y and can be thought of as the amount of variability inherent in the response before the regression is performed.
   • RSS measures the amount of variability that is left unexplained after performing the regression.
   • Therefore TSS-RSS : var explained after the regression.
   • Hence, R-squared measures the proportion of var in Y that can be explained using X.
   • R-squared = correlation.

MLR

Important Qs

1. Is at least one of the predictors useful?
2. Do all the predictors help to explain Y, or is only a subset of the predictors useful?
3. How well does the model fit the data?
4. Given a set of predictor values, what response value should we predict, and how accurate is our prediction?

Relationship between Y and Xs

When n is large, F close to 1 might still provide evidence against null hypo.

Given these individual p-values for each variable, why do we need to look
at the overall F-statistic? After all, it seems likely that if any one of the
p-values for the individual variables is very small, then at least one of the
predictors is related to the response. However, this logic is flawed, especially
when the number of predictors p is large.

Hence, if H_0 is true, there is only a 5 % chance that the F-statistic will result in a p-value below 0.05, regardless of the number of predictors or the number of observations.

Decide on important variables

Variable Selection: AIC and BIC and Adjusted R-squared.

• Forward Selection: Start from Null. Fit p SLR and add to null model the variable that results in the lowest RSS.
• Backward Selection: Start from all. Remove the variable with the largest p-value (the least significant).
• Mixed Selection: p-values can become larger as more predictors. Hence. at some point conduct backward selection.

Model Fit

RSE and R-squared : the fraction of variance explained.

1. R-squared
   • In MLR, = Cor (y,hat(y))^2
   • In SLR, = Cor(y,x)
   • Will always increase with more variables - as it increase the accuracy of the model by adding more training data.
   • If the variable significant, it will bring substantial increase in the R-sq.
2. RSE
   • more variables can have higher RSE if RSS is small relative to the increase in p

Predictions

Uncertainty associated with prediction:

1. The inaccuracy in the coeff est. is related to the reducible error. Use confidence interval to determine the closness to true population regression plane.
2. Model Bias: potential reducible error that may come from the model. But we ignore and operate as if the model is correct.
3. Even if knows the TPRP, irreducible error makes impossible to accurately estimate the response value. Hence use prediction interval. It is always wider than CI as it both covers the irreducible and reducible.

Use CI for Y over a large num of cities. While use PI for Y over a particular city.

The coefficients and their p-values do depend on the choice of dummy variable coding —> use F-test.

Extensions

Important assumptions betwenn predictor and response are

1. Additive Assumption: the effect of changes in a predictor on the Y is independent of the values of the other predictors
   • Synergy Effect = Interaction Effect : spend newspaper and TV half can be better than putting all money in one place.
   • Use interaction term —> if X1X2 term has low p-val, then it means X1 and X2 (the main effects) are not additive each other (share the effect)
   • if we include an interaction in a model, we should also include the main effects, even if the p-val associated with their coeff are not significant.
2. Linear Relationship: using polynomid regression to accommodate non-linear relationship which still allows to use linear system.
   • Include polynomial functions of the prdecitors in the model to improve the fit
   • Unnecessary predictor makes the model wiggely, which casts doubt whether that additional variable makes the model more accurate.

Potential Problem

1. Non-linearity of the response-predictor relationships

   • Residual Plot - tool to identify non-linearity. Due to multiple predictors, plot residuals vs predicted (or fitted) y.
   • The presence of a pattern —> some aspect of the linear model.
   • If non-linear association, use non-linear transformations of the predictors such as log X, sqrt(X), and X^2

2. Correlation of error terms

   • If correlation exists, estimated SE will tend to underestimate the true SE. Hence, PI gets narrower, p-val is lower which could cause errorneously conclude that a parameter is statistically significant.
   • In short, lead unwarranted sense of CI in the model.
   • Time series data: Residual plot, if error terms are positively correlated, tracking in the residuals - adjacent resi may have similar valuse.

3. Non-constant variance of error terms

   • SD, CI, Hypothesis test rely upon this

   • heteroscedasticity: funnel shape in the residual plot.

   • Solution: transform results in a greater amount of shrinkage of the larger responses, leading to a reduction in heteroscedasticity.

     

4. Outliers

   • Usually has no effect on the least square fit. But has significant effect on RSE which is used for CI and p-values —> important for the interpretation of the fit. + R-sq declines as well.
   • Use studentized residuals: each residual / ESE. ≥ 3 is outlier
   • It may imply missing predictor, so be aware.

5. High-leverage points

   • Removing high leverage has more substantial impact on the least squares line than removing an outlier.

   • It may invalidate the entire fit —> better remove it.

   • Leverage Stat: ≥ (p+1)/n —> suspect

     

6. Collinearity

   • predictors are closely related. Use Contour plot of RSS for visual.

   • Small change in the data could cause the pair of coeff values that yield the smallest RSS, the smallest LSE, to move anywhere along the valley. It is a great deal of uncertainty in the coeff est.

   • It reduces the accuracy of the esitimates of the regression coefficients, hence, increases the SE of hat(predictor).

   • It reduces the t-stat hence affect the hypothesis test weak (the probability of detecting a non-zero coeff).

   • Use Variance inflation factor (VIF): value of 1 indicates the absence of collinearity. Exceeds 5 or 10 —> problematic amount of collinearity.

     

Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Why Estimate f?

1. Prediction: hat(y) represents prediction of y.
   1. reducible error: imperfect estimate of hat(f) of f - can be fixed by using SL to estimate f.
   2. irreducible error: error introduced by random error term cannot be reducible no matter how well estimate the f. larger than zero:
      1. as there are some useful variables not considered in predicting y.
      2. There are unmeasurable variation that may change day by day.

Parametric Methods

• make an assumption about the functional form.
  1. stick to esitmating the chosen form instead of testing all of the others; know what u need.
  2. Uses the training data to fit or train the model. For linear → least squares.

Assuming a parametric ease the entire process compares to trying to fit the model into arbitrary forms. It may not match the true form of the function, which can be fixed by flexible model (it requires far more parameters though). But this flexible model can also be overfitting (follw the errors or noise too closely).

Non-parametric Methods

• Do not make explicit assumptions about the f form. seek an estimate of f that gets as close to the data points as possible.
  • Pros: potential to accurately fit a wider range of possible shapes for f (모양을 가정하지 않기떄문에)
  • Cons: large # of observations is required.

Wrong amount of smoothness may result in overfitting - as it does not yield accurate estimates.

Tread offs in flexi and interpreta

• IF interested in inference → more restrictive model is more interpretable. ⇒ difficult to understand how individual predictor is associted with the response.
• Interested in prediction: moderate flex and interpret is better due to the possibility of overfitting.

Supervised vs Unsupervised Learning

• Unsupervised: lack a response variable that can supervise our analysis.
  1. Cluster Analysis: whether the observations fall into relatively distinct groups → each group may differ.
     • Not be expected to assign all of the overlapping to their correct group (too crowded).

Will be covered in the different chapter.

Regression vs Classification

1. Quantitative - Numerical Values
   • regression Problems
2. Qualitative - K different classes or categories.
   • Classification Problems

The differene is vague. Both can be co-used in various methods. Although tend to select via type of response varaible (패러미터의 타입은 중요하지 않음).

Measuring the Quality of fit

Measure of how well its predictions actually match the observed data. In the regression setting, it is MSE.

Interested in predicting unseen test observation (whether it is future event or not) which is not used to train the model. Consider Degree of freedom and MSE results for finding suitable methods.

• we observe a monotone decrease in the training MSE and a U-shape in the test MSE. This is a fundamental property of statistical learning that holds regardless of the particular data set at hand and regardless of the statistical method being used.
• As model flexibility increases, training MSE will decrease, but the test MSE may not. When a given method yields a small training MSE but a large test MSE, we are said to be overfitting the data.

Bias-Variance Trade off

• Variance: amount by hat(f) would change if we used different training data set to estimate it. x의 변화에 민감하게 그래프가 꺾임. Least Square (straight line) has inflex, low variance.In general, more flexible methods have higher variance.
• Bias: error that is introduced by approximating a real-life problem. Linear regression (straight line cannot explain real life) results in high bias but also could estimate accurately via cases.Generally, flexible → less bias.

Classification Setting

equal = 1, inequal = 0

• Above equation computes fraction of incorrect classification = training error rate as computed based on our training data for the classification.

• Test error rate. A good classifier = one has small test error rate. = Misclassification error rate.

• Bayes Decision Boundary: line that assign each test data sets into categories it belongs to.
• It has the smallest error (in the population).
• In real life, not know the conditional distribution of Y given X. so impossible to use.

K-Nearest Negihbors

k-최근접 이웃 알고리즘

• attempt to estimate the conditional distribution then classify to get highest estimated probability.

1. Identify K points in Tr that are closed to x_0 represented by N_0.
2. Estimates conditional prob for class j as the fraction of points in N_0 whose response values eq j.
3. Applies Bayes Rule and classifies with the largest prob.

As K grows, the method becomes less flexible and produces a decision boundary that is close to linear. This corresponds to a low-variance but high-bias classifier.