
Reference:
- An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
- https://godongyoung.github.io/category/ML.html
Resampling
Extract sample from training data set, and apply series of models.
Application of several models will allow users to estimate which “region” will our models be when the data gets changed.
Cross-Validation
Test error and training error are different.
- Lowering the test error (data that was not given) is the goal.
- Training error is the error in the given data that can be underesitimated due to overfitting.
There are two ways of esitimating test error (often future prediction case)
- Indirectly infer test error by mathematical edition on the training data set (AIC, BIC).
- Hold out some training data to directily infer test error (Cross-Validation).
The vaildation set approach
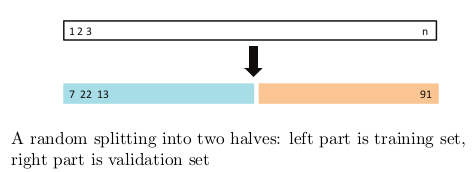
Hold out half of training set randomly — picked data is called vaildation set.
- 반을 자르기 때문에 어떻게 잘리느냐에 따라 모델 변동과 test MSE 도 심하게 변함
- Use remainder training set to get error rate (ususally MSE) about vaildation set and infer test error rate.
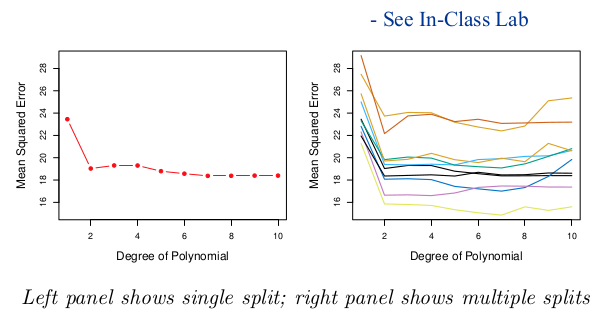
Degree of polynomial 이 에러를 줄이는데 도움이 안됨을 알 수 있다.
- 어떻게 잘렸는지에 따라 test MSE와 degree 또한 확연하게 달라진다
- 반을 잘랐기 때문에 추정 성능 또한 감소한다 - 반으로 적합하다고 모델을 정의 하면, 전체 자료를 적합했을 때는 test MSE가 크게 나올수 밖에 없다 (overestimate 한거니까). 반으로 전체를 예상할수 있다고 한것
Leave-one-cut Cross Validation (LOOCV)
한개의 자료를 빼고 이 자료에 대한 error rate 을 계산하는데, 이 계산을 모든 자료에 반복한다.
Training MSE is unbiased to Test MSE but has huge variance. Random error 를 포함하고 있어 이로 인해 분산이 생기는것. 이 분산들을 보완해주는게 validation 이다. validation으로 분산을 줄이지만, 약간의 bias가 생긴다. 이 약간의 편향된 모델들을 평균냄으로써 분산이 줄어드는것
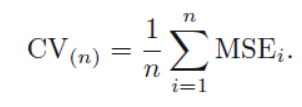
- 데이터 반을 가지고 하는것에 비해, test MSE에 대한 training data가 거의 정확한 추정이 가능하다. 이는 overestimate 하지 않으며 bias가 적음을 의미한다
- Validation set approach 와 다르게 항상 같은 결과가 나온다.
K-fold Cross-Validation
가장 대중적으로 test error rate 구할때 사용하는 방법이다. 최선의 모델이나, 최종 선택된 모델에 관한 테스트 에러에 대해 이해하는데 사용된다.
Validation set approach 는 너무 단순하고 LOOCV는 손이 너무 간다 (하나하나 적합해야 하니까). 이 중간지점이 k-fold CV. k 그룹으로 랜덤하게 데이터를 나눈다. 한 그룹을 뺴고 적합해 MSE 구하는것을 k번 반복한다 (LOOCV 처럼). 이후 K로 평균을 낸다.
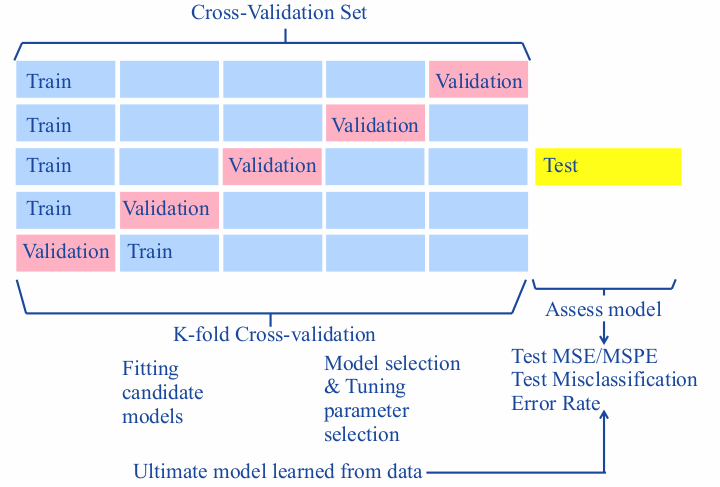
k = n 일경우 LOOCV와 같은식이다.k-fold CV는 LOOCV에 비해 더 간결하고 빠르게 계산을 함에도 불구하고 성응에서 큰 차이를 보이지 않는다 (좋은쪽으로). 즉 LOOCV의 장점들을 다 가지고 있다. 또한 bias-variance trade off에서 LOOCV보다 더 강점을 가지고 있다 (다음 항목 참조)
Bias-Variance Trade off for k-fold CV
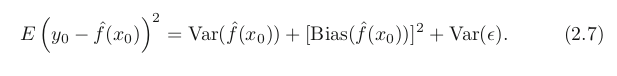
위 식에서 알 수 있듯 test MSE는 bias 만으로 결정 되는것이 아니다. Variance의 관점에서 (위에 서술하였듯) LOOCV 보다 k-fold CV가 더 좋다.
- LOOCV는 낮은 bias와 높은 variance를 가지고 있는데 이는 적합시의 데이터 n-1개중 n-2가 동일한 데이터 (두개의 적합에서 2개를 제외한 나머지 데이터는 재사용된것들) 따라서 재사용을 많이한 n개의 모델들는 highly correlated 되었기 때문이다. highly correlated —> higher variance (overfitting과 비슷한 개념)
- 이로 인하여 덜 겹치는 k-fold CV가 더 낮은 분산을 갖는것이다
CV on Classification Problems
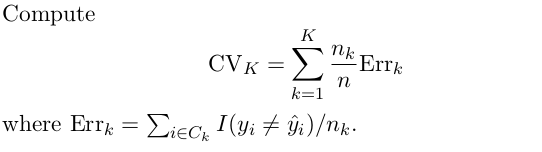
식이 조금 달라졌다. 이전까지의 계산은 데이터 수에 대한 양적 변수를 가정한 CV였고 위의 식은 질적 변수에 대한 식이다 (질적 테스트는 error rate를 의미한다)
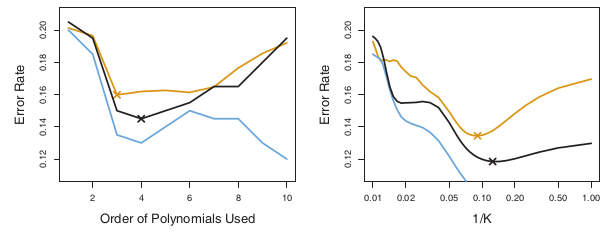
검은색 선이 10-fold CV인데 파란색인 training error에 비해 테스트 에러를 잘 잡아주고 잇는 모습이다. 저 테스트 에러는 진짜 테스트 에러로 (시뮬레이션 데이터를 이용한) 실 상황에서는 구하지 못하는 경우가 많은 선. 따라서 위 그래프는 진짜 에러 비율에 대해 k-fold CV가 어느정도로 잘 잡아주는지 보여주는 것.
Bootstrap
실제로 계산하기 어려운 uncertainty 들을 계산하는데 쓰이는 강력한 기법이다. 선형희귀의 계수 분산의 경우 표준편차 정도는 구할 수 있지만 이에 대한 정확한 통계량은 구할 수 없는데, bootstrap은 이를 가능케 한다. 또한 이 방법은 분포를 미리 가정하지 않은 (실상황처럼) 상태에서 사용 할 수 있기 때문에 더 강력한것.
밑의 식은 a, 1-a를 각 두 회사에 비율 투자할때, 분산을 (risk) 최소화 할 수 있는 비율을 찾는식이다.
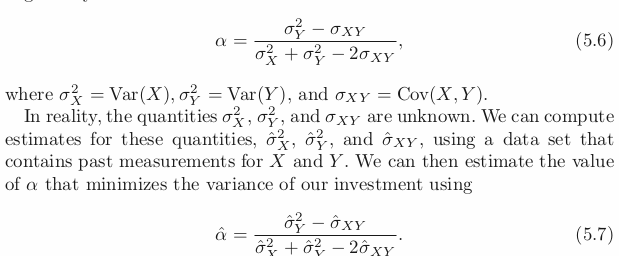
위와 같은식을 사용 할 수 있는 이유는 아래와 같이 가지고 있는 데이터들을 복원추출 하여 새로운 샘플들을 계속 만들어 내기 때문. 밑의 식을 반복하여 큰 수인 n 개의 샘플들을 만들어 이에 대한 추정량 hat(a)가 생기는것.
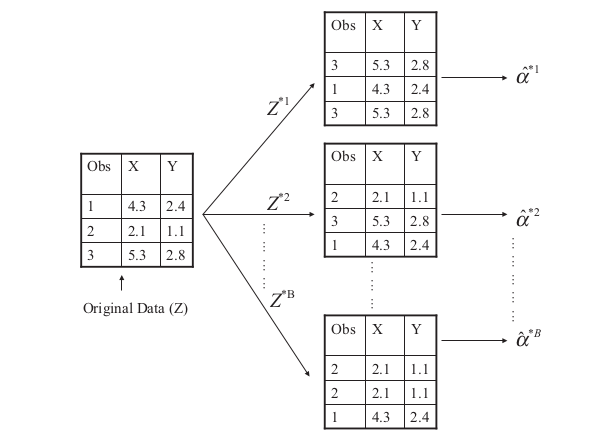
위의 식을 이용하며 추정량에 대한 standard error 또한 구할수 있게 된다.
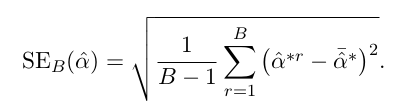
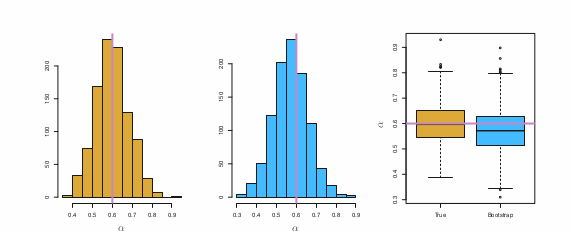
노란색이 모든 자료들을 가지고 반복 추출해서 구한값, 파랑색이 bootstrap으로 하나의 data set만으로 반복추출해서 얻은 결과이다. 매우 비슷함을 알 수 있는데, bootstrap이 적은 data set으로 구하기 힘든 통계량의 특성까지고 구사 한다는것을 알 수 있다.
Bootstrap for Prediction Error?
bootstrap 샘플의 경우 원래 데이터 들과 많이 겹치게 되는데, 이로 인해 true prediction error 을 많이 underestimate 하게 된다. 마찬가지로 원래 데이터들을 훈련 샘플로 쓰고 bootstrap의 데이터들을 vaildation 에 쓰게 되면 안 좋은 (쓰레기 같은) 값이 나온다.
이에 대한 데이터 셋 겹침을 구할수 있으나, 매우 복잡해지고 이로 인해 결국 CV가 prediction error를 예상하는데 더 나은 방식이 된다.
정리하자면 Test error rate을 구하는데는 bootstrap. Prediction error을 구하는데는 CV.


