Reference: Barry Wilkinson, Michael Allen - Parallel Programming_ Techniques and Applications Using Networked Workstations and Parallel Computers (2nd Edition) -Prentice Hall (2004)

Barrier

• A particular reference point for processors which no one can proceed until every processors (or stated number) get to the point.
• Commonly when processes need to exchange data and then continue.
• Once the last one has arrived, inactive processes are awakened.
• Apply both shared memory, and message-passing systemss

Barrier - MPI

• MPI_Barrier(MPI_Comm comm) is called by each process and return once everyone arrives.
• Naturally synchronus, and message tags are not used.

Counter Implementation

Called a linear barrier as well. Counting the number of processes is handled by a single counter.

• Implementations must handle possible time delays for eg. two barriers in quick succession.
• There are two phases:
  • Arrival Phase : Send msg to master and stay inactive or idle as not all are arrived.
  • Departure Phase : Receive from master and released.

— Remember Send() is not the blocking (depend on the buffer size), but Receive() always do the blocking. Cost = O(p) for time and computation complexity

Tree-Based Implementation

• Use of decentralized tree construction.
• Arrival and Depature order is reversal as it supposed to be.
• Since it is up and down, O(2 lg p) = O(lg p) for communication time.

Note: broadcast does not ensure synch in terms of a global time

Butterfly (Omega) Barrier

Pairs of processes sync at each stage as following

1. 01 23 45 67 (4 has 4,5)
2. 02 13 46 57 (4 has 4,5,6,7)
3. 04 15 26 37 (4 has 0,1,2,3,4,5,6,7)

After the stages, every processes are synchronized and can continue. O(2 lg p) = O(lg p) for communication time.

Local Synchronization

It can be formulated for only essential synchronization among few processes, instead of being “wastefully” idle — In a mesh or a pipeline and only neighbours sync. Not using barriers, but ues Receive to communicate and idle certian processes to exchange its data.

DeadLock

It will occur using synchronous routines (or blocking routines without sufficient buffering) if both performs the send first to each other. In general, assign even-numbere in send first, odd-numbered in rece first coule bo a good solution.

MPI_Sendrecv() and MIP_Sendrecv_replace() —> deadlock prevent commands.

Data Parallel Computations

• ease of programming
• ease of increase to larger problems.

  1 2 3 4 5 6 7 8 9

  forall (i = 0; i< n; i++){ a[i] = a[i] + k; } // In SIMD, those particularly designed for these, implicitly has barrier itself // If MP computer using library routines, generally explicit barrier is required. // Following is an example i = myrank; // myrank is a process rank between 0 and n-1 a[i] = a[i] + k; /* body */ barrier(mygroup) // consider the barrier overheads as it may longer than its body

  Synchronous Iteration

Parallel started at the beginning of the iteartion, yet each processes cannot proceed to the next iteration unless all the assigined tasks in the iteration is completed.

Jacobi Iteration: all x are updated together.

• guess X, and iterate while hope it converges.
• In converges if tha matrix is diagonally dominant.
• Terminates whin convergence is achieved (subtract of two is within the error tolerance)

야코비 방법

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

// Sequential 
for (i=0; i < n; i++){
	x[i] = b[i]; //b[] holding the constants
}
for (iteration = 0; interation < limit; iteration++){
	for (i = 0; i < n; i++){        // n number of rows and cols.
   		sum = -a[i][i] * x[d]         // Jacobi method excludes itself.
   		for (j = 0; j < n; j++){      // each row summation iteration
   			sum = sum + a[i][j] * x[j]  // summation of one row
   		}
        new_x[i] = (b[i] - sum) / a[i][i] //a[i][i] cannot be zero
    }
   	for (i=0; i<n; i++} x[i] = new_x[i] //data move
}
// Parallel
i = process_id;
x[i] = b[i];                      // assign each process array	for (iteration = 0; interation < limit; iteration++){
for (i = 0; i < n; i++){          // n number of rows and cols.
    sum = -a[i][i] * x[j]         // Jacobi method excludes itself.
   	for (j = 0; j < n; j++){      // each row summation iteration
  		sum = sum + a[i][j] * x[j]  // summation of one row
    }
   	new_x[i] = (b[i] - sum) / a[i][i] //a[i][i] cannot be zero
    broadcast_gather (&new_x[i], new_x); //spread and gather data over processes
    global_barrier();
    for (i=0; i<n; i++} x[i] = new_x[i] //data move
}

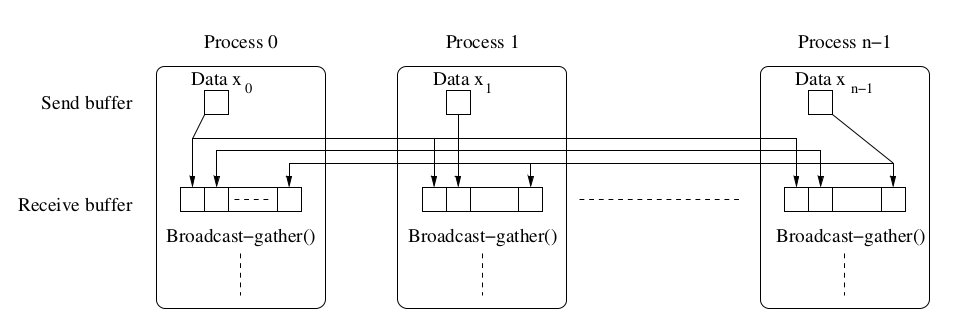
Broadcast_gather expect all the processes to have matching routines. Hence further implementation must be made to avoid deadlocks whet each prcoss can stop once it met its tolerance (so each has diff num of iterations). It can be easily replaced with send and recv().

Analysis

Heat Equation

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

// Sequential Code
for (iter = 0; iter < limit; iter++){
	for (i = 1; i < n; i++){
		for (j = 1; j < n; j++){
        	q[i][j] = 0.25 * (h[i-1][j]+....);
        }
    }
   	for (i =1; i < n; i++){
   		for (j = 1; j < n; j++){
   			h[i][j] = g[i][j];
   		}
    }
}
    // Parallel Code
for (iter =0; iter < max_iter; iter++){
	g = 0.25 * (w + x + y + z+);
	send(&g, ...)
	...
	...
	...
	recv (&z, ...)
}

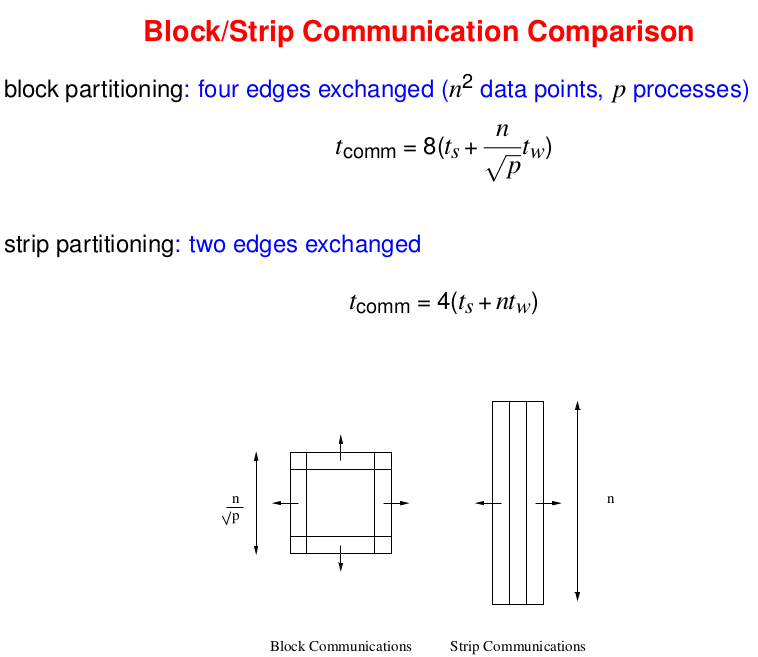
• Block Partitioning: Each process generates and receives 4 messages each —> hence total of 8.
• Strpi Partitioning: Two edges where data points are exchanged. Each edge generates and receives 2 messages —> hence total of 4.

In general, strip partition is best for a large startup time, and a block partition is best for a small start up.

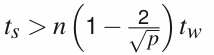
For p ≥ 9, if above equation is fulfilled, the block partition has a larger communication time.

Safety & Deadlock

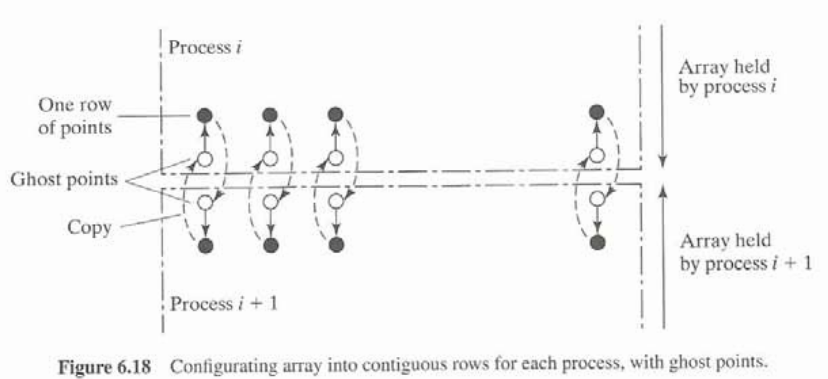
As it is unreliable to assume the internal buffer will be enough, there are two methods.

1. Switching send and recv in different order as mentioned couple of times so far.
2. Implement Asynchronus communication using ghost points.

Assign extra receive buffers for edges where data is exchanged. It is typically translated as extra rows and columns in each process’ local array (known as halo). In this buffer, asynchronus calls such as MPI_Isend() can be used.