
Reference:
- An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
- https://godongyoung.github.io/category/ML.html
Why Not Least Square?
OLS 는 오차의 평균이 0, 오차의 분산이 등분산 (모두 비슷함), 그리고 오차가 서로 관계가 없는 선형 모델중에서 최적이다. 또한 분포가 정규분포일 경우, OLS estimator 는 Maximum Likelihodd estimator 와 같은 결과를 낸다.
OLS는 unbiased 한 대신 variance하고, 이로 인해 데이터에 따라 변동차이가 크다. 하지만 다음과 같은 이유로 OLS를 대신하는 대체 방법들이 존재한다.
- 예측정확도:
- OLS는 가정된 분포가 어느정도 맞고, 변수의 개수 p보다 자료의 개수 n이 훨씬 많을때 좋다.
- 만약 n이 p 보다 (보통 3배) 많지 않다면, OLS는 큰 변동성 (variance)를 가지게 되고, 이로 인해 새로운 자료에 대해 예측을 잘 못하는 overfitting 이 나타난다. variance = p * (SD/N) 이므로, p가 클 수록 증가한다.
- 만약 n이 p 보다 적으면, OLS는 variance가 무한인 사용 불가능한 방법이다. 이 이유는 matrix 연산에서 full rank인 matrix만 가능한데, n<p는 비가역행 행렬 (non full rank) 가 된다.
- 해석력:
- OLS는 Y에 전혀 관계가 없어도 0으로 제외할 수 있는 능력이 없다. 즉 중요한 변수를 선택하고 무쓸모한 변수를 제외하는 능력이 없음. 그래서 5장에서 사용한 방법들이 존재하는것.
Options?
- Subset selection: 유의미한 변수를 골라내고 OLS 하는것
- Shrinkage: 모든 변수들을 이용하여 저합한다. 계수들인 OLS에 비해 0으로 가려고 하는 경향이 있다. 자동적인 변수 선택도 가능하게 한다.
- Dimension Reduction: p개의 차원 (변수)에서, m의 차원 (변수)로 projection 후 OLS 하는 방법.
Subset Selection
Best Subset selection
모든 경우의 수를 써보고 최고를 찾는법. 하지만 p가 클수록 ovrefitting 된 모델을 고를 확률도 늘어남.
- 변수 p개 중에서 0 ≤ k ≤ p 인 모델 모든것을 계산 하는 방법
- 각 k개의 모델들중 R^2 이 가장 높은거 선택 (변수 수가 같으니 간단하게 찾기 가능)
- 뽑힌 모델들중 최고를 뽑는것. 변수의 갯수가 달라 R^2은 이제 못쓰고 CV-error, AIC, BIC, Radj 등을 쓴다.
다시 말하지만 변수의 수가 많을 수록 설명력이 당연히 강해지고, 이로 인해 low training error값인 R^2이 좋게 나올수 밖에 없다. 하지만 우리의 목표는 테스트 에러지, 트레이닝 에러가 아니다.
이 방법은 계산양이 많다는 단점이 있다.
Stepwise Selection
Best Subset selection의 단점인 계산양과 잘못된 모델 선택의 대안으로 사용 가능한 방법이다.
- Forward Selection: 보수적인 모델 (변수가 최소화된) 을 선택함
- backward selection: 변수가 많이 들어간 모델을 선택함
- mixed selection: 제일 best subset selection과 비슷한 모델을 찾아줌
이 세가지 방법들은 best 모델을 찾는것이 보장되어 있지는 않다. 세세하게 다른 차이점이 존재한다.
Choos Optimal Model
test error를 최소화 하기 위한 방법이 두가지 가 존재한다.
- Overfitting 을 고려한 수학적 보정을 통안 test error의 간접 추정
- Traninig est중 몇개를 빼서 하는 직접 추정 (5장에서 배운것들)
간정 추정들로는 CV-error (C_p), AIC, BIC, adjusted R^2 이 존재한다.
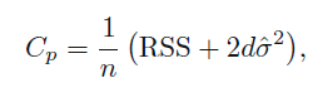
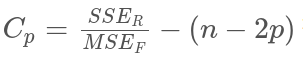



위에서 RSS = SSE_r (reduced model SSE)를 뜻한다.
Validation and Cross-Validation
예전에는 컴퓨터의 계산 능력으로 위의 방법들을 선호 했지만, 이제는 CV를 더 선호한다.
위의 방법과 CV는 몇개의 그룹으로 잘렸는지, 혹은 데이터가 어떻게 나뉘어졌는지에 따라 변동될 수 있어, 선택된 변수 숫자가 최적의 모델이 아닐수 있다. 이를 해결하기 위해서 one-standard-error rule을 적용한다.
Test MSE 의 SD의 SE 를 구한뒤, 최소 Test MSE에서 SE만큼 떨어진 모델들을 고려하는것이다. 즉 최소 Test MSE 의 갯수가 4이면, 앞뒤로 1개씩 더 총 3개를 고려하는것이다.
Shrinkage Methods
모든 변수로 적합하되, 계수들을 0으로 constrain 혹은 regularize하는 방법이다. 이 방법은 추정된 계수들의 (hat values)의 variance를 대폭 줄여준다는 장점이 있다.
Ridge Regression
기존의 RSS + 모든 계수 합의 제곱 * 람다 의 값을 최소화 하는 식이다. 따라서 계수들이 점점 줄어든다.
이 방식으로 데이터 적합성을 올리는 동시에 계수들을 0 으로 가게한다. 다만 이 계수는 intecept 값을 포함하지 않는다.
람다 값이 커질수록 shrinkage 효과에 더 비중을 두는 식이다. 이 람다 값은 CV를 통해 결정하며, 0일때는 기존의 OLS와 똑같다.
주의해야 하는점은 이 추정되는 계수는 람다에만 영향을 받는게 아니라 변수들의 스케일링에도 영향을 받는다. (애초에 그 계수가 어느 스케일링을 기준으로 만들어진거니까) 따라서 표준화 작업을 해주고 시작을 하게되면, 모든 변수들의 표준편차는 1이 되며, 이로 인해 Ridge regression이 스케일링에 영향을 받지 않는다.
Why Ridge?
람다가 증가함에 따라 flexibility는 감소하고 Variance가 감소하고 Bias는 증가하게 된다
즉 Bias Variance Trade off 에 있는것이다.
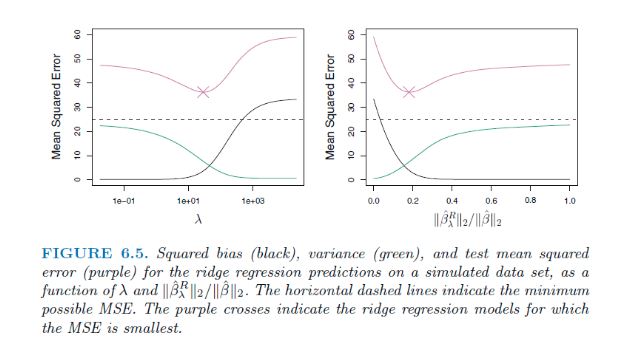
Bias는 람다값의 변화에 따라 조금씩 바뀌지만, Variance의 경우 람다가 증가함에 따라 큰폭으로 감소한다. 이는 람다라는 제약에 따라 계수들이 shrinkage 하면서 변동이 크지 않는 모델이 나온다는 의미이다. (점점 람다 값에 미미해져가는거).
선형에 가까울때
- OLS: unbias 하지만 variance가 높고, 이는 데이터의 변동에 계수가 크게 변동한다는 의미이다. 또한 p>n 일때 OLS는 유일한 해가 없다 즉 모델을 만들때마다 값이 다 다르게 나오는거
- Ridge: 약간의 bias 손해소 varaince 를 크게 줄인다. p>n 일때 덜 flexible한 적합을 통해 소수의 데이터 특성에 국한되지 않는 모델을 만드는것. 또한 람다 계산은 한번만 하면돼서 best subset selection에 비해 계산이 간편한 장점이 있다.
Lasso
Ridge의 단점
Ridge Regression의 방식은 예측과 관련해서는 아무런 문제가 없지만, 해석측면에서 약점을 가지고 있는다. 만약 해석의 경우 1,2,3 변수만을 통해 하고 싶다고 하자. 다만 Ridge는 모든 변수로 적합을 해야만 하고, 나머지 계수가 0이 아니다 (0에 가깝다) 즉 1,2,3 변수만을 통한 해석이 쉽지 않은것.

적당한 람다 값으로, 몇몇 계수를 정확하게 0으로 만들어서 ridge 보다 더 강령한 해석이 가능한것 (나머지 불필요한 계수들이 모델에서 사라진것이니까). 따라서 Ridge보다 더 적은 변수들을 포함하기에 sparse model 이라고 한다.
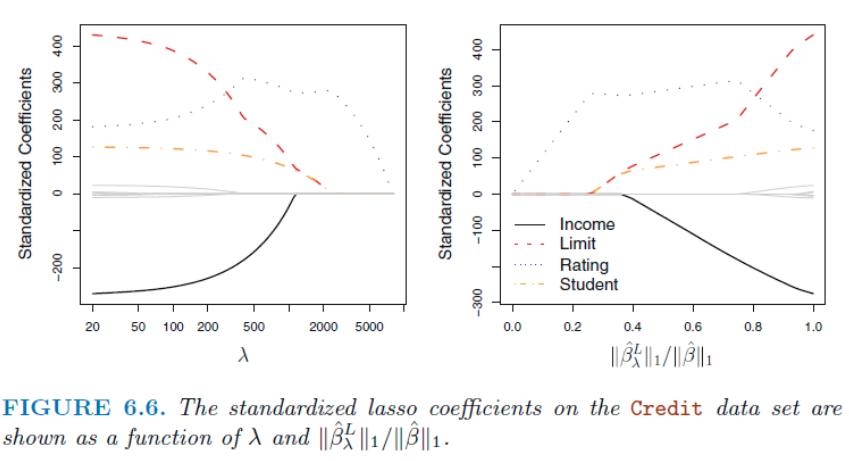
Ridge와 다르게 위에서 rating 계수만 끝까지 남아 있다가 사라진다. 즉 람다 값이 올라감에 따라 변수들이 차례차례 0이 되어 버리므로, 원하는 계수들만 가지고 있는 람다값의 선택이 가능한것. Ridge 는 꾸준히 같이 함께 줄어든다 (마치 비율처럼).
다른 식
위의 Ridge, Lasso, best subset selection 은 다른 식으로 표현 가능한데, 식들을 살펴보면
Lasso and Ridge는 Best subset selection을 실현 가능한 형태로 대체한 식임을 알 수 있다 (즉 계산의 부담을 덜은점). 특히 Lasso는 명확하게 변수를 없앤다는점에서 Best subset과 더 유사하다.
Lasso 변수 선택 성질
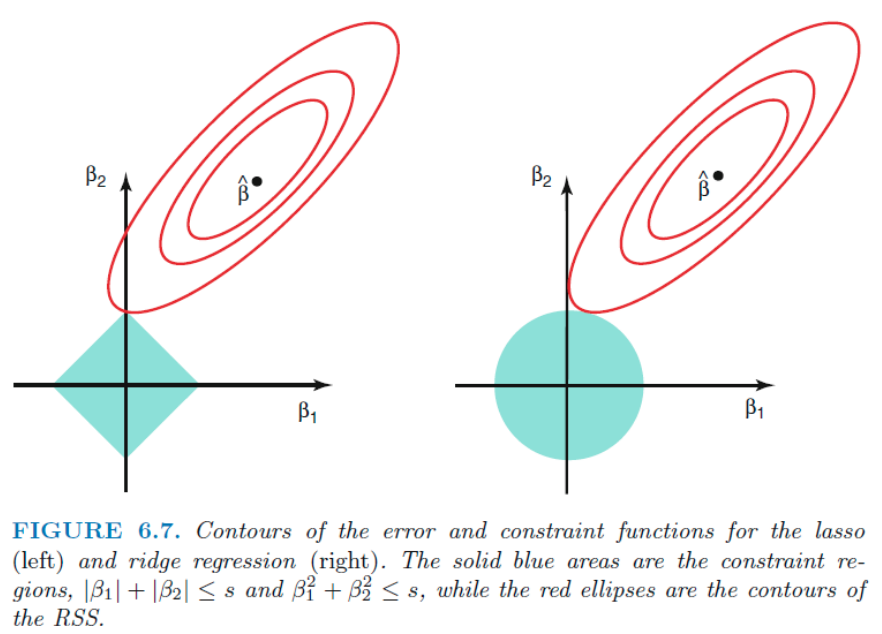
빨간선이 RSS, hat value는 OLS점이다. 만약 s 가 충분히 커서 hat value를 포함하면, 이는 OLS와 같은 값을 가지게 된다. 즉 hat value는 해당 제약범위 (초록색)과 가장 작은 RSS와 만나는 지점일 것이다.
Lasso는 사각형의 모양이라, 다른 계수가 0인 지점에서 쉽게 교점이 생긴다. b2 축에서 교점이 생겼으므로 b1 = 0 이 된다. 하지만 Ridge의 원 모양은, 한 계수가 정확히 0인 교점이 생기기 힘들다. 즉 한놈만 선에 닿는 일이 벌어지기 힘들다. 왜냐면 공평하게 퍼지니까.
Lasso and Ridge 차이점
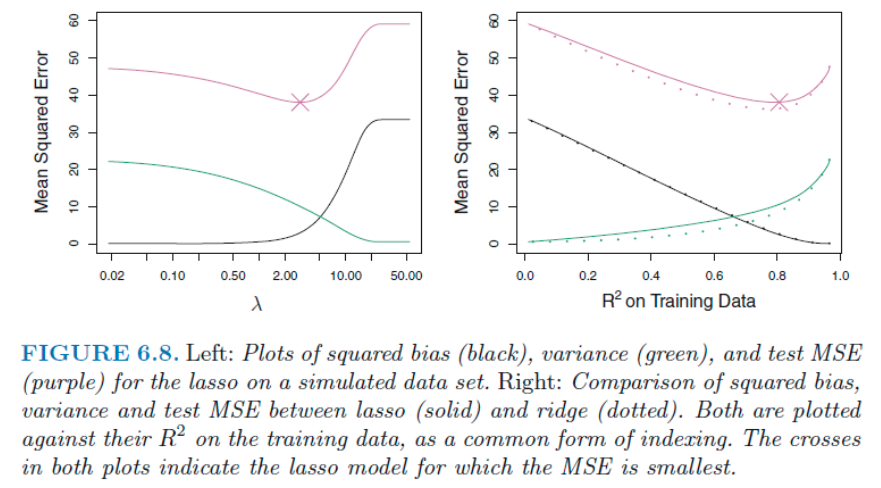
해석력은 Lasso가 변수들을 완전히 제외시킴으로써 더 쎈거는 이제 알게 되었다.
오른쪽 그림에서 두 방법 모두 bias는 비슷하지만 ridge의 variance가 약간 더 낮아서 Test MSE가 Lasso 에 비해 더 낮다. 하지만 이 경우는 모든 데이터가 Y값과 관련이 있는 (correlated)한 데이터 였다. 이에 따라 몇 계수들을 제외한 Lasso 가 불리하다.
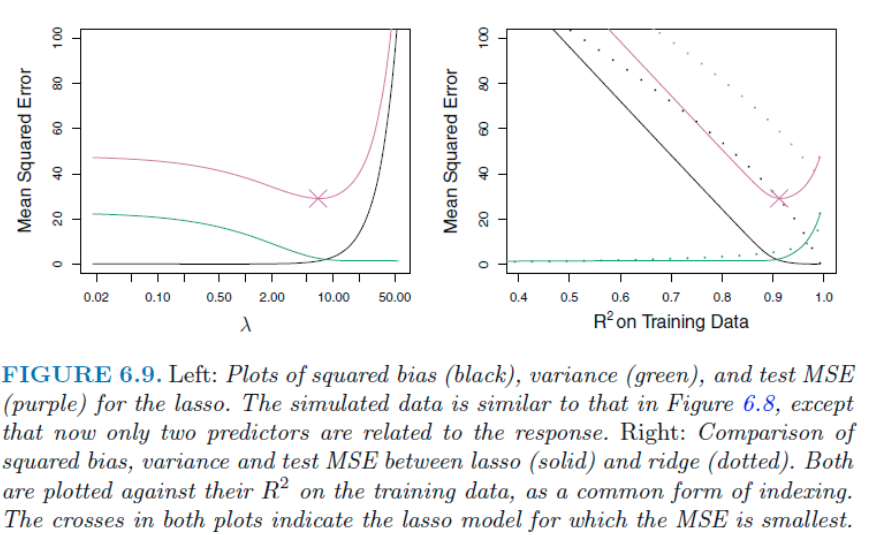
위 처럼 만약 2개의 변수만이 유리하다면, Lasso 가 Test MSE를 더 낮은 값을 가진다. 즉 두 방법의 성능은 데이터 상황에 따라 다른것이다. 이를 알기 위해 CV 방법을 사용한다.
람다값 정하는 방법
몇몇 람다값을 선정해서 CV해보고 이중 가장 적은 CV-error를 가진 값을 선정하고, 이 계산에 쓰인 데이터를 원래 총 데이터에서 빼서, 새로운 데이터에 뽑은 람다 값을 이용하는것이다.


