
Reference:
- An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
- [ISL] 6장 -Lasso, Ridge, PCR이해하기
Dimension Reduction Methods
앞서 공부했던 방법들은 몇 변수만 선택하거나, 계수들을 0으로 줄이는 방법과 같은 variance를 줄이기 위함이었다. 차원축소 방법은 변수 자체를 변환하여 분산을 줄이는 방식이다
기존 p개의 변수들에서 m의 변수들을 이용한 Least Square 를 이용한 적합을 하는것 (M<P)
이처럼 제약이 있는 상태에서 계수를 정하면 bisa가 생기나, 이로 인해 variance가 눈에 띄게 감소 되므로 결과적으로는 더 좋은 모델들이 만들어지는것이다.
Principle Components Regression
Principal Components Analysis (PCA)
n*p의 크기를 가지고 있는 x를 줄이기 위해 데이터들의 변동(분산)을 가장 잘 나타낼수 있는 first principal component direction을 찾는다 (이 선이 분산의 크기가 가장 크다)
이 계산 과정에서 데이터 중심에 축을 두고자 centering을 하게 되는데, 이 방식은 분산에 영향을 미치지 않아 결과는 같게 된다.

물론 분산의 무한함을 방지하기 위해 두 계수의 제곱합은 1과 같다라는 제약을 걸어 두었다
이렇게 만들어진 Z1 = principal component score라고 불린다.
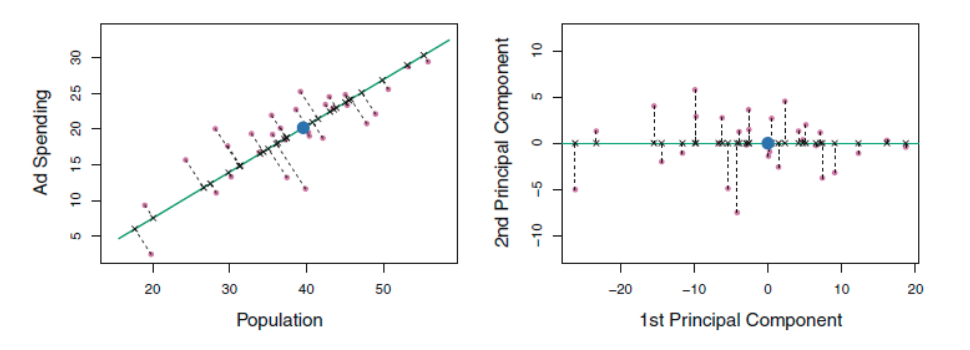
왼쪽의 초록선은 데이터가 가장 큰 분산을 가짐과 동시에, 모든 n개의 관측값에 가장 가까운 선이기도 하다 (즉 수직 점선들의 거리가 가장 짧게). 파란점은 (pop,ad) 의 평균 값을 의미한다. 오른쪽의 그림은 2차원으로 표현된 왼쪽 그림은 회전시켜서 1st PC의 방향이 x축과 같아지게 만들은것. 이 1st PC의 값은 결국 저 파란점과의 거리를 의미하며, 음수이면 두 평균값보다 낮고, 양수일수록 두 평균값보다 높은것이라고 해석을 할 수 있는것.
위의 왼쪽 그래프에서 볼 수 있듯, 두 변수는 선형관계를 가지고 있는데, 이를 파악하여 정보를 압축한 1st PC는 각각의 변수에 대해 강력한 선형 관계를 보여준다.
p개의 변수는 곧 최대 p개의 다른 component를 만들 수 있음을 의미하는데,
2nd PC의 경우
- 1st PC와 uncorrelated
- 1st PC가 미처 설명하지 못한 부분
에 대해 설명 할 수 있는 방향, 즉 1st PC의 제약 하에 가장 분산이 큰 방향으로 linear combination이 결정된다. 위 오른쪽 그림에서 수직선들에 대해 2nd PC가 사용된것이
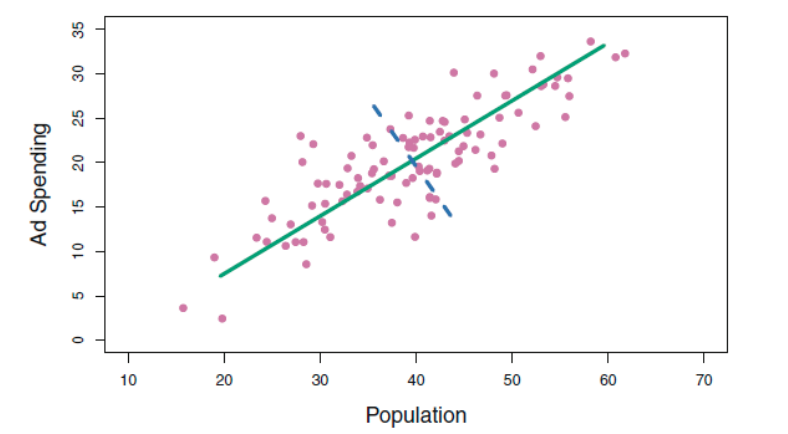
왼쪽 그림에서 이와 같이 표현될수 있다. 초록색이 첫번째, 파랑이 두번째 PC
이 두 PC는 (두 선은) 직교 (90도)를 유지하는데, 이는 두 관계가 zero correlation임을 의미한다. 현재는 변수가 2개여서 2개만 있지만, 더 높은 다차원은 여러 방향의 선으로 분산이 가장 높은 방향의 선을 긋는다.
저 위의 오른쪽 그림에서 보이듯, 1st 에 비해 2nd의 값의 수치가 훨씬 적다는 것을 확인 가능하다 (1st는 -25 ~ 20, 2nd는 -10~10). 지금은 변수가 두개여서 불가능하지만, 여러 변수가 있는 상황에서 이와 같은 형태는 차원을 축소 할 수 있다는 것을 의미한다 (1st가 대부분의 정보를 포함하니까 굳이 2nd까지 가지고 있을 의미가 없지). 따라서 차원을 축소함에 따라 이전 compnent에 비해 uncorrelate하면서도 variance가 가장 큰 방향으로 component를 결정 가능하다.
Principal Components Regression Approach (PCR)
PCR은 PCA를 통해 만들어진 M개의 예측변수들을 통해 Least Square적합을 하는것.
“p개의 변수를 가장 큰 variation으로 나타낼수 있는 direction 은 Y와 연관이 있을것이다” 라는 가정하에 이루어지는 분석이므로, 이 가정이 항상 참일수는 없으나 대게의 경우 좋은 적합을 보여준다. 또한 가정이 맞을 경우, 전의 p개의 변수보다 더 적은 m개의 변수를 사용하므로 overfitting을 완화할 수 있다. (n이 p보다 크지 않다면 - 데이터가 변수갯수보다 일정이상 크지 않다면 least square의 변동성이 큰 결과를 내고 overfitting이 커짐을 다시 기억하자)
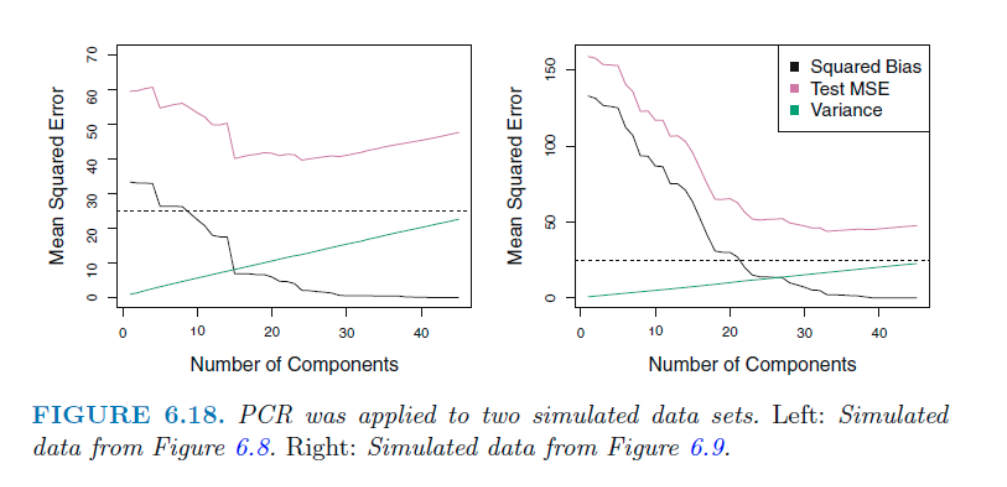
저번 블로그에서 마지막에 나왔던 데이터에 관한 PCR결과이다. 왼쪽의 경우 45개의 변수중 45개 모두가 유의미한 데이터인 경우, 오른쪽의 경우 2개의 변수만 중요할 때이다. 더 많은 component를 사용할 수록 bias decreases, but variance increases
45개의 component 사용한 값은 단순히 Leaner Square에 모든 변수들을 사용한 것과 같은 값을 보여준다. 왼쪽의 경우 15개 정도의 component에서 성능 증가를 보인경우에 비해 오른쪽은 훨씬 더 많은 component를 가져야 TEST MSE가 낮아졌다.
이는 PCR의 가정, 몇몇의 component로 데이터의 분산을 잘 나타낼 수 있고 Y의 관계가 있을것이다, 이 충족될때 큰 성능을 발휘하기 때문이다.
PCR은 변수 선택법이 아니고, 모든 기존의 p개의 변수가 선형결합으로 포함된 변수이다. 이는 PCR이 Ridge의 continuous version이라고 할 수 있다.

Partial Least Squares (PLS)
앞의 PCA는 unsupervised 방식으로 Y값을 전혀 고려하지 않았다. 이 방식은 PCR의 단점을 곧 의미하는데 (PCA를 이용했으니까 PCR이) 예측 변수들의 관계를 가장 잘 설명하는 방향이, 반응변수 (Y)를 설명하는 예측 변수들의 관계를 가장 잘 설명하는 방향이 아닐수도 있다는것.
PLS는 이 방식을 보완했는데, 같은 방식이지만 M개의 변수들을 supervised해서 만들어 내는데, 이로 인해 반응변수와 관계된 변수들의 관계를 더 잘 나타낼수 있는것.

PCR과 마찬가지로, PLS역시 변수들을 표준화한 후 계산해야하고, 몇개의 direction을 만들것인지는 cross-validation을 통해 알아본다. 그러나 실제에선 PLS는 supervised라는 점에서 bias는 줄여주지만 그에 상응하여 variance가 높아지기에 PCR이나 Ridge만큼의 성능을 보이지 못하는 경우가 많다.


