
Reference:
- An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
- https://godongyoung.github.io/category/ML.html
선형 모델: 모델의 단순성으로 해석과 추론이 쉽다는 장점. 하지만 이러한 가정한 현실적인 문제에 대한 예측을 하기에는 터무니 없는 가정.
따라서 이와 같은 선형가정을 완화시키되, 해석과 추론력을 최대한 잃지 않는선에서 예측력을 증가 시키는 방법들에대해 배워본다.
- Polynomial Regreisson: 다차항을 이용하여 선형 모델을 확장
- Step function: K부분으로 변수를 나누어서 constant를 생성하는 방법
- Regression splines: 위 1,2 방식의 확장으로 K부분으로 나누어 각 부분에 다차항을 적합하는 형식이다. 각 부분은 양 옆의 범주에 대해 매끄럽게 만들어야 한다는 제약이 있지만, 적당한 범주로 나눈다면 유연한 적합이 가능하다
- Smoothing penalty: 위 3번과 비슷하지만 매끄럽게 한다는 제약을 최소화 시키는 방식
- Local Regression: 3,4 번과 비슷하지만, 각 범주가 겹칠수 있다. 이로 인해 유연한 적합이 가능한것
- Generalized additive model: 여러개의 예측 변수들에 적용하는 방법
Polynomial Regression
예측변수의 전체 구간에 non-linear 형태를 부여하는 방식
단순하게 각 변수를 다차항의 형식으로 넣어준 방법이다. X2 = X1 ^ 2 과 같은 형식.
일반적으로 3,4차 이상으로 포함시키지는 않는다.
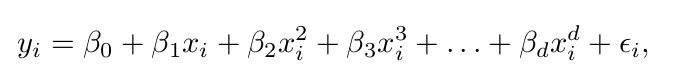
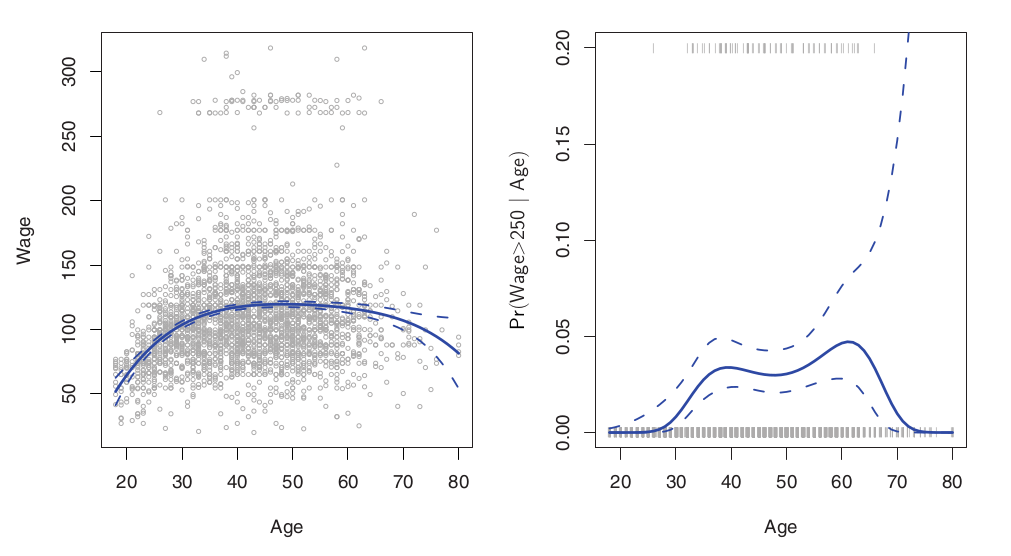
왼쪽: Least Square 4차 적합. 오른쪽: 왼쪽의 250이상의 고소득자에 대한 Logistic 4차 적합. 점선들은 예측값의 분산을 통해 구한95%의 confidence interval
예측값의 분산은 다음과 같이 구할 수 있다

Logistic의 경우 확률을 반환한다는것을 기억하자. 고소득층에 대한 데이터는 79개에 불과하여 신뢰구간이 매우 넓게 나옴을 확인할 수 있다.
Step Functions
전체 X를 몇개의 구간으로 나누고 일정한 상수를 부여하는 방식
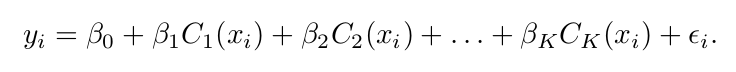

절편인 b0 는 Y값의 평균이고, 나머지 b 들은 각 구간에 속한 데이터의 평균과 b0와의 차이를 의미하게 된다. C1 ≤ X ≤ C2의 평균값 - b0 = b1. 이러한 각각의 계수들은 마찬가지로 least square로 적합하여 구한다. 각 더미 변수에 대한 (C들은 더미 변수이다) 분산/신뢰구간은 3장 참조
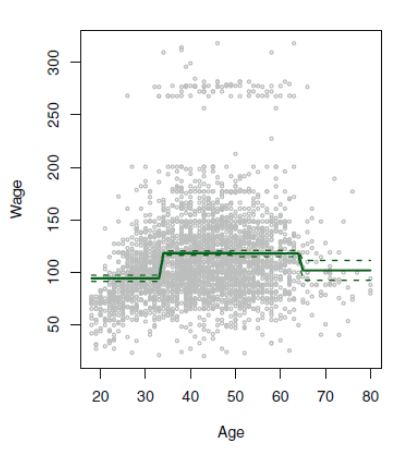
예측값에 자연적으로 부분을 나눌수 있는 지점이 존재 하지 않는다면, 이 방식은 옳지 못한 방향을 나타낼 수 있는데, 명확하게 증가 추세인 구간을 제대로 구분지어주지 않는다면, 이 증가 추세를 반영하지 못하기 때문이다. 위 그래프에서 나이가 들수록 월급이 올라가는 증가 추세를 반영해주지 못한 상황이다.
Basis Functions
앞의 두 방식은 Bisis funciton의 특별한 형태라고 볼 수도 있다.
앞선 두 방식과 다르게, 선형 모델로 X를 적합하지 않고 다음과 같은 모델에 적합한다.
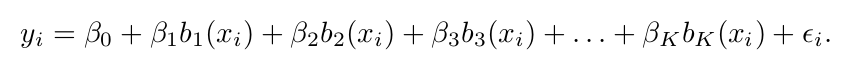
각 b의 값은 이미 정해져 있으면 알려진 상태임을 명시하자. 이 말인 즉, 우리는 사용할 함수를 미리 선택해 놓는다는 의미이다.

Regression Spines
Piecewise Polynomials
맨 위 1번 Polynomial regression 처럼 전체 X에 대한 다항적합을 하는 형식이 아닌 몇개의 범주에 대해 비교적 낮은 차수의 적합을 따로따로 하는것을 piecewise polynomial regression 이라 한다.
계수가 바뀌는 지점을 knots 라고 하는데 (서로 다른 부분을 묶는거니까) 삼차 다항식에 이 knots가 없다면 결국 그건 그냥 보통의 평범한 삼차항이다. 다음은 knots가 한개 존재할때의 3차항이다.
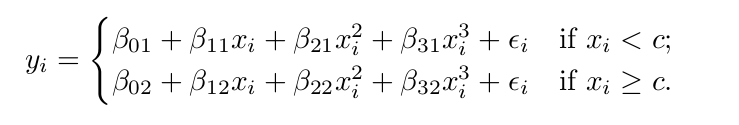
즉 c를 기준으로 2개의 부분으로 나누어 각각의 부분에 다항적합을 한것이다. 이 모델의 degreef of freedom = 8 이다 (각각 4개씩)
하지만 이 형식은 중간의 knots 들을 부드럽게 연결하는 제약이 없기때문에 다음과 같은 말도 안되는 모델이 탄생하게 된다 (1번).
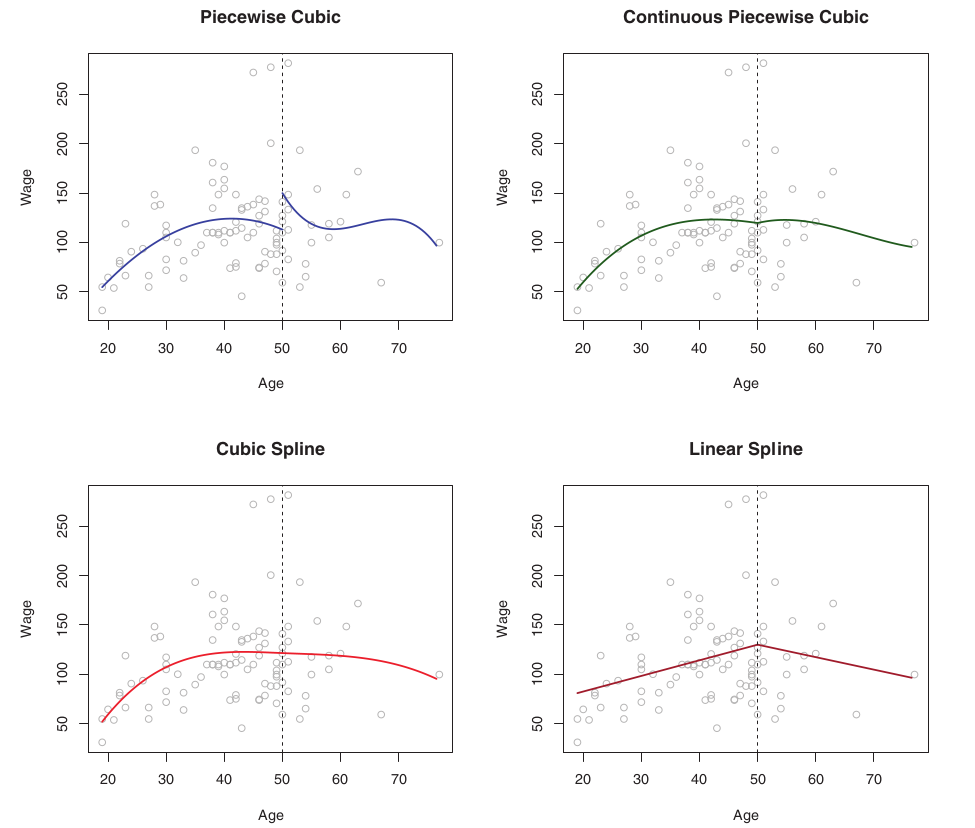
Constraints and Splines
1번의 그래프에서 나이가 50일때 갑자기 월급이 폭등하는 것은 말이 안된다. 이에 50부근의 선들을 연결해 준 그래프가 2번이다 (continuous piecewise cubic). 하지만 이 또한 꺽인듯한 부분을 볼 수 있는데 이러한 약한 제약을 (50 부근 이어준것) 가지고는 다른 그래프에서 v자 형태로 나올수 있기에 고쳐주어야 한다. 이 부분을 부드럽게 해주기 위해 1,2차 미분을 해주어야 한다. 즉 50부분에서 continuous + smooth (1차 2차 미분) 라는 세 가지의 제약을 적용한것이 3번 그래프.
이러한 제약은, 자유도를 하나씩 잃음을 의미한다. 따라서 1번에서는 자유도가 8, 2번에서는 7, 3번에서는 5이다. 보통 cubic spline uses 4 + K df (K = num of knots).

Splines Basis Representation
d차 적합을 하면서 d-1차 까지의 미분을 달성하기 위해서는 basis function 을 올바르게 선택해야 하는데, 이는 trucated power basis funciton 을 이용하면 된다.
다음은 cubic spline을 cubic regression에서 만드는 방법이다.
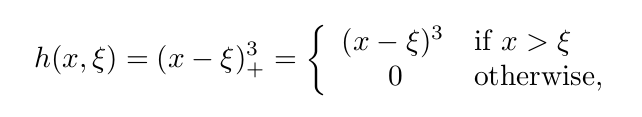
위의 뱀처럼 생긴것이 knot을 의미한다. 위의 식을 각 knot마다 추가하는것이다.

하지만 위와 같은 방식으로 구할 경우, 양 끝에서의 예측 신뢰구간이 넓어지므로 예측의 정확도가 떨어지는 현상이 나타난다. 원래 모든 모델의 분산은 양 끝에서 커지지만 non-linear 적합을 시도한 이 경우에 (which has more flexibility) 분산이 더 커지게 된다.
이러한 현상을 고치기 위해 맨 양쪽의 knot 이후에 있는 부분의 경우 선형 적합을 하여서 문제를 완화시키는데 이를 Natural Cubic Spline이라 한다.
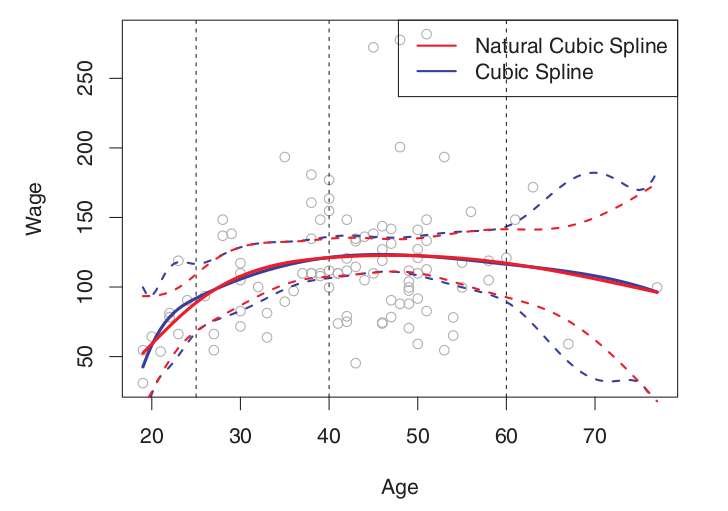
위의 그래프를 보면 수직 점선 (knot) 이후에 빨간 점선이 분산을 적게 가지고 있음을 볼 수 있다. 이러한 양끝쪽에 3차 적합이 아닌 1차 적합을 하기에 자유도를 2씩 잃어서 K+4-(2*2) = K df.를 가지게 된다.
Num and Location of the knots
이제 knot를 어떻게 사용하는지 알았으니 몇개를 어디에 사용해야 하는지를 알아야 한다.
적정한 df를 설정하고, 이에 따른 균등한 quantile에 knot를 배정하는 형식.
결국 df (자유도)를 몇으로 설정하지가 문제인데, Cross-validation을 이용하여 CV-error 값이 가장 낮은 자유도의 갯수를 사용한다
Comparison to Polynomial Regression
보통 Polynomial Regression의 경우 flexible 하기 위해 차수를 엄청나게 높이고는 하는데, 반대로 regression spline의 경우 차수는 유지하되, knots를 늘리는것으로 유연해진다. 따라서 대부분의 경우 regression spline이 produces more stable estimates. 또한 급변하게 변하는 부분에 대해서 우리가 따로 더 많은 knots를 부여함으로써 (반대로 원만하면 knots 수 줄이고) 유연성을 적절하게 조절 할 수 있기에 더 좋다.

위의 polynomial의 경우 15차 항인데, 이로 인해 끝쪽이 매우 요동친다.
Smoothing Splines
Overview of Smoothing Splines
Regression과 다르게 Smoothing은 모든 x에 knots를 두기에 갯수나 위치 지정의 문제가 없다!
결국 우리가 원하는 사항은 RSS를 작게 만들면서, 부드러운 함수를 찾는것.
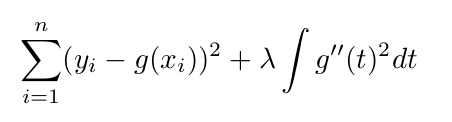
위 식의 왼쪽 부분이 RSS이다. 이러한 형태는 Loss (잘 적합) + Penalty (변동이 크지 않게) 식인데, Lassor and Ridge에서 사용되었던 형태와 비슷하다.
오른쪽의 식은 t부분에서의 변화도를 나타내주는데, 변화도가 음수일 경우도 있으니 제곱을 해준다. 람다 값이 커질수록 더 부드러워질것이다.
람다가 0이면 모든 데이터를 지나가고, 무한하다면 선형 (굴곡이 없는 직선 - 선형회귀와 같다). 결국 람다 = bias variance trade off 정도를 조정하는 값인것이다.
이 람다가 3차에서 최소화 될때는 위에서 이야기 했던 2차 미분이 가능한 knot를 가지고 양 끝이 linear 한 natural cubic spline이다. 물론 이와 정확히 같은 값의 식이 나오는게 아니라, 비슷한 형식의 shrink된 함수

Choosing lambda
In smoothing spline, lambda controls the smoothness. Hence, the effective degrees of freedom changes depending on the value of lambda. 람다가 0에서 무한까지 변할때 effective df는 n에서 2까지 변한다.
기존의 자유도는 pramater의 갯수로 계수의 수를 뜻했다. 따라서 smoothing spline은 명목상 n개의 자유도를 가지고 있지만, 이들인 이미 shrink 되도록 constrain (제약)을 받고 있기에, 이 제약의 정도에 따라 flexibility가 다르다. 따라서 정확히 어느정도의 자유도를 실질적으로 가지고 있는지를 나타내주는것.

Regression 과는 다르게 람다를 어느 값으로 할지가 남아있다 (RSS를 최소화 하는). 물론 Cross-validation 을 이용한다.

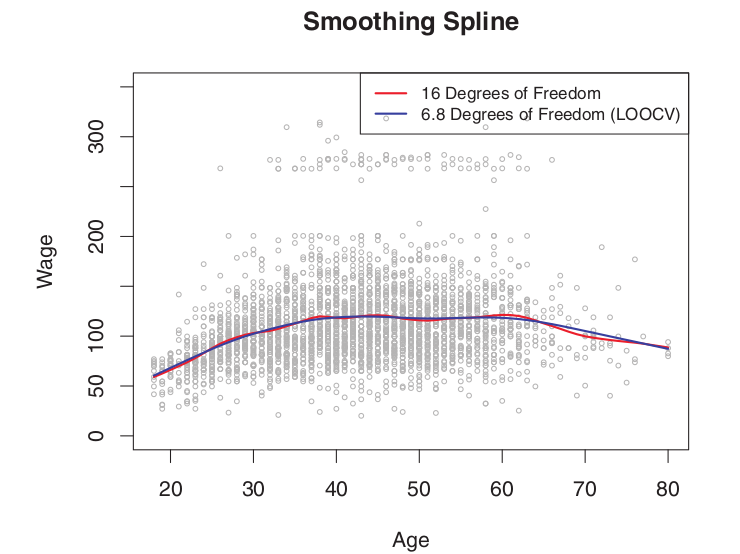
임의로 정한 effective df 인 16에 비해 계산으로 나온 6.8 이 거의 유사한 형태를 보여주고 있다.
Local Regression
각 특정 타겟 포인트 근처의 관측 자료들만을 토대로 적합시켜 flexbile하게 하는 방식

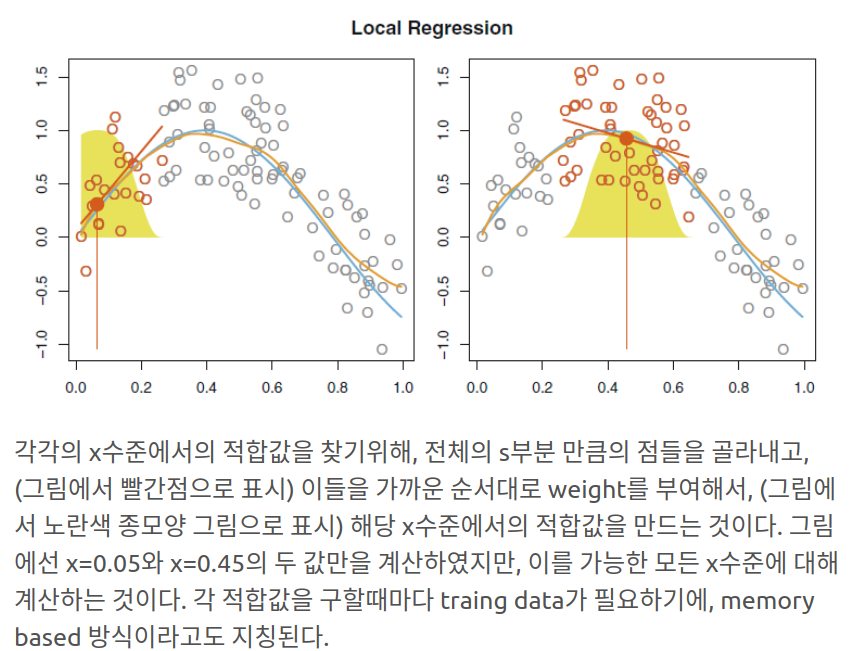
위에서 중요한 사항은 얼마나 많은 이웃들을 볼것인지 즉 s를 몇퍼센트로 설정할지이다. s가 작을수록 더 지역적인 (조그만) 부분으로 꾸불한 선이 나올것이다 물론 이 s 또한 cross-validation 을 통해 찾는다.
Local Regression은 p-차원에서 p가 3이나 4보다 훨씬 클 경우, 굉장히 안좋은데 이는 대체로 트레이닝 데이터가 굉장히 적음을 의미하기 때문이다. Nearest Neighbour Regression의 경우도 같은 단점을 지니고 있다.


