Reference:

1. An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
2. https://godongyoung.github.io/category/ML.html

Why?

Tree-based는 regression과 classification을 위한 방법으로, 예측변수의 전체 공간을 단순한 여러 영역으로 계층화 (stratifying) 혹은 분할 (segmentation)하는 방법이다.

예측: 해당 영역의 training data의 평균값이나, 최빈값에대해 예측한다

이 방식은 단순하고 설명력이 좋은 반면에, supervised (chapter 6,7)에 비해 예측력이 떨어지나, 이를 보완하기 위해 bagging, random forests, boosting과 혼합하는데, 위의 방법들을 사용하면 다중트리 (multiple trees) 드링 생성된다. 이 다중트리는 합의 예측을 제공하기에 나중에 하나로 결합된다. 이로 인해 예측정확도의 엄청난 상승을 가져온다. 하지만 이로 인해 해석이 다소 어려워질 수 있다.

Decision Trees

Decision Tree는 regression and classification 모두에 사용된다

Regression Trees

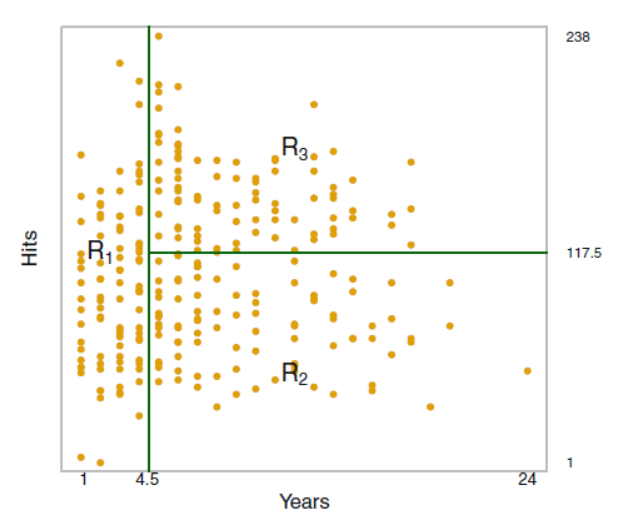
각각의 노드 (R1,2,3)들은 terminal nodes or leaf of tree 라고 부르며 그 전까지의 노드들 (리프가 아닌 중간 단계)은 internal node 라고 부른다.

위에서 보면 알 수 있듯, 메이저리거의 경우 년차가 연봉을 정하는데 가장 중요한 역할을 하고 있음.

이처럼 Decision Tree는 설명력 측면에서 강점을 가지는데, 위의 그림으로 시각적 설명이 가능하다.

Prediction via Stratification of Feature Space

1. 모든 X (변수) 가 포함된 공간을 J 개로 겹치지 않게 나눈다

   1. RSS를 최소화 하는 방향으로 위의 그림처럼 박스형식으로 쪼갠다.

   2. 물론 무한한 박스 조합이 가능하기에 Top-down or greedy 방식을 사용한다.

      1. 당장의 RSS를 최소화 하는것을 목표로 한다 (greedy) - recursive binary splitting 이라고 칭한다.

2. s 는 cutpoint 로 RSS가 최소화 되도록 영역을 밑의 두가지로 분할하는 점이다.

   

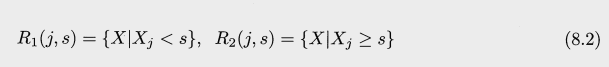
3. 다음의 식이 최소화 하는 j (공간 갯수) 와 s를 찾는다

   

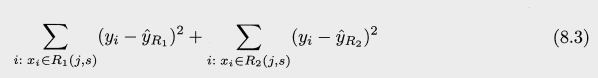
   5. 위의 첫 식으로 만들어진 두 영역중 하나를 선택해 같은 방식을 적용하여 3개의 영역이 된다. 이와 같은것을 계속해서 반복하며, 설정해둔 stopping criterion 을 만족할때가지 진행한다. 예를 들어 한 영역당 관측치가 5개 이상이어야 한다등의 조건.

4. 각 공간에서 training data 평균을 통해서 일관된 예측값을 반환한다. 모든공간에 같은 예측을 시행한다.

Tree Pruning

위의 방법은 훈련셋에 좋은 예측이 가능하지만, 데이터 overfit의 가능성이 높은데 이는 지나치게 세분화된 tree는 training set 의 특징또한 포함할 수 있기 때문이다. 이로 인해 test set에서 성능이 좋지 않다.

분할 수가 적다면 편향성이 약간 증가하지만 분산이 낮아져 해석하기 쉬울것이다.

위에서 설명한 방법을 보완하는 방법은 어느 threshold 까지만 리빌딩일 진행하도록 하는것. 이는 작은 트리를 (분할 수가 더 적은) 만들수는 있지만 short-sighted (근시안)적인데 왜냐면 초기에는 좋지 않아 보인 분할이 나중에 가면 좋은것일수도 있기 때문이다.

더 나은 방법은 큰 트리 T0 를 만든뒤 이 트리를 다시 prune 하여 subtree를 얻는것. 그렇다면 어떻게 prune 하는것이 좋은 방법인가? - 최종 목표는 lowest test error 를 갖는 subtree를 찾는것이지만 이에 대해 모든 CV는 불가능 하다.

이를 위해 Cost complexcity pruning (or called weakest link pruning) 을 사용한다. 가능한 모든 서브트리를 고려하는것이 아닌 조율 parameter a 로 다음식을 최소화 하는것

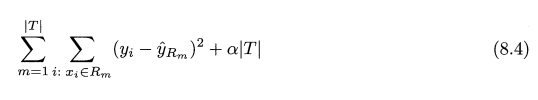
T = num of Terminal node, R_m = box corresponds to mth terminal node, hat(y)R_m = R_m 훈련 관측치들의 평균. a = 0 일 경우 subtree T = T_0.

1. 각 terminal node 에서의 RSS 를 줄여주는 loss-term (앞부분)
2. 지나치게 많은 terminal node 가 없도록 (복잡성늘 낮춰주는) penalty form (뒷부분)

위 두가지의 폼을 a로 비율적으로 조정하는것인데 이 a를 CV를 통해 구하는것.

최종 알고리즘

1. 모든 자료들을 이용해서 resursive binary split 계속해서 진행하여 stopping criterion 만족하면 멈춤 (full size tree) 이는 a = 0 일때의 트리와 같다.
2. 이렇게 최종적으로 만들어진 트리에 cost complexity pruning 을 적용하여 가장 좋은 서브트리들을 a의 함수로 얻는다.
3. K-fold 를 진행하며 a를 선택한다.
   1. 모든 훈련자료의 kth fold 의외의 fold 에 위 1,2번 반복
   2. kth fold 를 이용하며 나머지에 error 를 평균내서 validation error 가 가장 낮는 a로 결정한다
4. 3번에서 구한 a를 통해 1번의 트리 (처음 큰 트리) 에 pruning 을 진행한다 - 그러면 가장 좋은 서브트리를 선택한다!

Classification Tree

For a classification tree, we predict that each observation belongs to the most commonly occurring class of training observations in the region to which it belongs. 가장 많이 등장한 클래스로 분류. 따라서 클래스 비율또한 관심을 가진다.

recursive binary splitting 을 classification error rate 를 이용하여 시행한다.

Pmk = kth class에 나온 m 번째 영역내의 훈련 관측치들의 비율

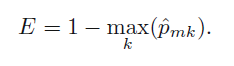
1 - (m 영역에서 여러 k들중 가장 많이 등장한 비율). 하지만 클래스간의 비율을 고려하지 않아 좋은 식은 아니다. 이를 보안하기 위해 Gini index or entropy를 이용한다.

지니는 impurity를 가장 낮게 가지는 클래스를 선택하여 진행한다. 마찬가지로 교차 엔트로피또한 m 번째 노드가 pure 할 수록 impurity 지수가 낮을것이고, 그것을 선택한다.

최종 pruned 된 트리에 대한 예측 정확도의 경우 위의 classification error rate 방법을 사용한다.

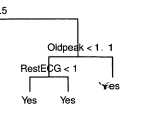
양쪽 모두 Yes (left: 7/11, right: 9) 인데 이는 지니와 엔트로피의 purity를 올려주기 때문에 분할한것. 즉 두개다 모두 Yes 이므로 분류오차를 줄여주지는 않는다.

Tree vs Linear Models

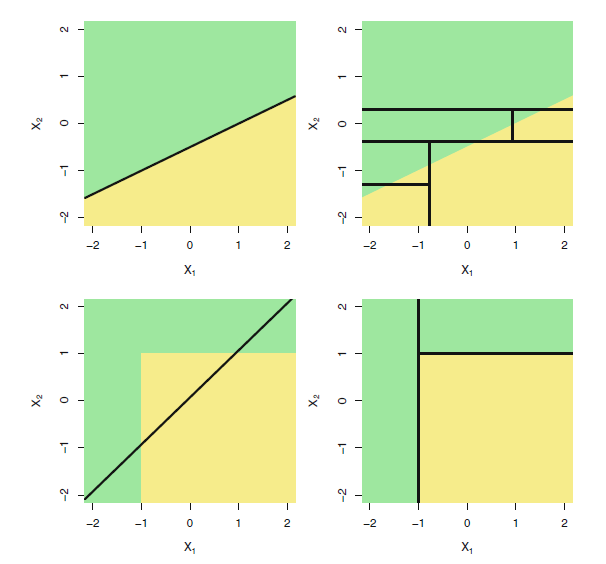
선형이라면 선형회귀,아니면 트리. 결국 때에 따라 다르다 맨위의 경우 선형이, 아래의 경우 트리가 더 좋은상황.

Pros and Cons of Trees

Pros:

• 설명하기 매우 쉽다 (linear 보다도)
• 인간의 의사결정 과정을 더 밀접하게 반영한다고 생각된다
• 그래픽으로 나타내기 쉬우며, 비전문가 또한 쉽게 해석 가능 (물론 크기가 작으면)
• 더미 변수를 만들지 않고서도 qualitative, quantatative 모두 가능

Cons:

• 예측 정확도가 좋지 못하다 - prune을 하더라도 overfit의 한계를 벗어나지 못하기 때문.
• ‘non-robust’ - 데이터의 작은 변화에도 트리의 최종 예측값이 크게 변동한다 (variance가 크다)

예측 정확도를 bagging. random forest, boosting 을 하여 향상 시킬수 있다.

Bagging & radom forest & boosting

Bagging (Bootstrap aggregation)

bootstrop 을 활용한 방식. Decision Tree 는 high variance (non robust) 하다는 단점을 가지고 있다. bagging 을 사용하여 variance를 낮추는것.

분산을 줄여 예측 정확도를 증가시키는 자연스러운 방법은 population으로 무터 많은 수의 training set 을 취하여 각각의 training set 별로 예측모델을 만든후, 이 예측결과들을 평균내는것. 물론 이 처럼 다수의 훈련셋은 보통 불가능 하므로, 붓스트랩을 사용하여 표본을 샘플링, 훈련자료들을 생성하는것.

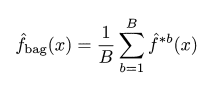
말 그대로 bootstrap 하여 (자료를 만들어서 예측하고) aggregating (평균내는것) 하는 방법.

Regression tree의 경우:

붓스트랩하여 훈련셋 B개를 만들어 B개의 regression tree 를 만들고, 이 예측 결과들을 평균낸다. tree 들은 prune 되지 않은 큰 트리들이다. 따라서 각각의 훈련 tree 들은 분산은 크되 편향이 작은 상태. 이 처럼 분산이 크고 편향이 작은 나무들을 모두 모아 평균하여 분산과 편향이 작게 만들어주는것.

Classification Tree의 경우:

똑같지만, B 개의 나무에 의해 예측된 클래스를 기록하여 이 예측간에 가장 자주 발생하는 클래스를 선택하는것.

• Out of bag Error Estimation
  • Bagging 은 bootstrap에 의해 복원추출에 뽑히지 않은 데이터들 (보통 1/3가 안뽑힘) 이 자동으로 validation set 되어 CV를 하지 않아도 test error의 추측이 가능한데. 이 뽑히지 않은 데이터들을 out-of -bag (OOB) 라고 부른다
  • 즉 뽑히지 않은 B/3 개의 모델들이 특정 데이터에 예측을 하고, 이 예측들을 평균낸다. 이 방법으로 OOB error and Classification error 를 구할수 있다.
  • B가 클경우 OOB 오차는 LOOCV의 오차와 사실상 동일하며, CV가 힘들만큼 데이터가 클때 유용한 방식이다.
• Variable Importance Measures
  • 여러 나무를 합하여 예측력을 올렸지만 (분산을 줄여서), 이로 인해 해석력을 잃었음. 왜냐면 이제 나무 한개가 아니니까.
  • Bagging 전만큼은 아니지만 RSS (regression), Gini Index (classification) 를 이용하며 전반적인 예측변수 중요도를 확인할수있다.
  • 모든 B개의 나무에대해 각 변수에서의 split으로 인한 RSS/Gini 가 감소한 정도를 측정하여 평균을 낸후, 가장 많이 감소하였으면, 해당 변수가 중요하다는것.

Random Forest

Bootstrap은 샘플링을 통하기에 correlation 이 높다 (서로 비슷한 모델이라는 뜻). 이로 인해 covariance가 높고, 그렇기에 bagging으로 인한 variance 감소가 크지 않다. Correlation을 줄인 bootstrap 방식이 바로 random forest 인것.

• 똑같이 bootstrap을 통해 B개의 나무를 생성한다. 하지만 split 할때 전체 p개의 예측 변수중 랜덤하게 m 개만 골라서 그 중에 또 split 기준을 만든다. 이후 계속해서 반복한다. 보통 m^2 = p 이다.
• m개는 결국 p개의 반도 안된다. 이는 한개가 강력하고 나머지는 적당한 예측 변수를 가정한다면, bagging 의 경우 모두 나무가 비슷비슷 하기에 가장 강력한 변수를 top split으로 뽑을것이고, 이로 인해서 bagged tree들이 모두 비슷해지는 효과를 만드는것. 앞에서 말하였든 highly correlate 된 통계를 평균 내는것은 correlate가 약한것들의 평균으로 얻는 variance감소보다 더 적다
• 이와 같은 현상을 피하기에 랜덤으로 뽑아서 다른 예측변수들도 (기회를 얻는것) 사용되게 하여 bagging 보다 결과적으로 decorrelate한 효과를 가지는것. 따라서 이 나무들의 평균으로 얻는 variance 감소가 훨씬 커진다.
• m = p 는 결국 random forest = bagging 이며 많은수의 변수들이 correlate 라면 sqrt(p)보다 더 적은 m 이 유효할 수 있다.

Boosting

강력하지는 않으나 보완에 초점을 맞춘 약한 모델 (weak leaner)를 결합해서 정확하고 강력한 모델 (strong leaner)를 만드는 것. 다른곳에서도 사용가능하나 decision tree만 이야기한다

Bagging 의 경우 bootstrap을 이용하여 데이터셋을 만든후, 개별적인 decision tree 생성인데 이 생성과정이 서로 관련이 없고 독립적이다. boosting 의 경우 tree들이 순서대로 만들어지는데, 각각의 tree는 이전 트리들의 정보를 이용하여 만들어진다. 즉 boosting 은 bootstrap sampling 을 사용하지 않는것. 대신 각 트리는 수정된 버전의 원래 데이터셋에 적합한다.

맨 처음에만 데이터에 적합을 하고, 그 이후부터는 이전 tree 의 residual에 적합하는것.

즉 boosting 의 경우 slowly learning method 이다.

Boosting tree에는 3가지의 hyper parameter 가 존재한다.

• Tree의 갯수 B: Boosting 은 variance 감소가 목적인 bagging 과 다르게 bias를 줄여나가는 방식이다. 따라서 B가 너무 크면 overfit이 될 수 있다. B 는 CV 를 이용하여 선택한다
• 반영비율 lambda: 각 step에서 배운것을 얼마나 반영할지 정해주는것. 보통 0.01/0.001 을 사용한다. 람다가 작을수록 더 큰 B 가 필요하다 (왜냐면 람다가 작다 = 매 스텝에서 (그 전 트리에서) 배우는것이 적다).
• Tree 의 split 갯수 d: boosting complexity 를 조절해준다. Complexity가 높으면 flexible하고 이는 variance 가 높고 bias가 작음을 의미한다. 위에 말하였는 boosting은 bias를 줄이는데 목표를 두고 있기에 complexity가 크지 않다 (왜냐면 overfit 위험이 생기니까). 때로는 d = 1 일때가 좋을수도 있는데, 이는 addtive model에 적합하기 때문. d = interaction depth라고 생각할수도 있는데 선형회귀의 X1X2 같은 여러 변수의 조합을 고려하는 tree node가 생기기때문.

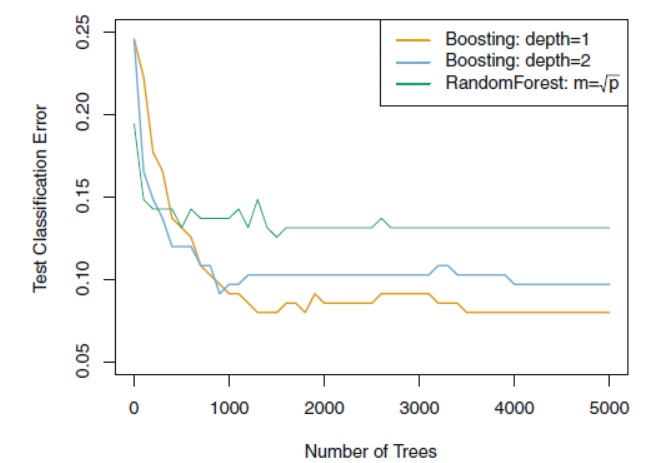
Boosting 은 이전 모델의 실수를 기반으로 만들어지기에 각각의 트리들이 작은 트리여도 충분한 경우가 많다.