
Reference:
- An Introduction To Statistical Learning with Applications in R (ISLR Sixth Printing)
- https://bkshin.tistory.com/
Unsupervised Learning
The challenge
이전 챕터들에서 supervised Learning 에 관해서 여러가지들을 배웠다. 만약 이진 결과값을 데이터로 부터 도출하여 추측하여야 한다면, 로지스틱, LDA, classification Trees 등을 이용하여 값을 도출하고, 이 결과값에 대하여 어떻게 접근해야 할지에 대한 명료한 지식들을 배웠다 (CV, validaton…)
반면에 unsupervised learning 의 경우 조금더 어려운데 이는 대부분의 실험들이 주관적이고, 분석 (예측)과 같은 간단한 목표를 가지고 있지 않기 때문이다. 대신 unsupervised learning은 exploratory data analysis 에 대한 부분으로 행해진다. 또한 결과값을 도출하는데도 어려움이 있을수 밖에 없는 이유가 이 모델이 맞는지에 대해 테스트 할 수 있는지에 대한 방식이 존재하지 않기 때문이다 (예를 들어 예측하는데에 대해 예측할 값이 존재하지 않는다던가)
PCA
correlated variables가 많은 데이터를 마주 하였을때 principle component (PC)를 이용하여 더 적은 변수들로 대부분의 variability를 summarize 하여 설명할 수 있게 해준다. 챕터 6에서 이야기 하였듯, PC directions는 본래의 데이터에서 highly varaibla한 방향을 보여줌과 동시에 데이터 클라우드에 대해 가장 가까운 선과 부분 공간을 보여준다.
PCR을 사용하기 위해서, 우리는 PC를 예측 변수로 사용한다. 이 PC를 이용해 supervised 한 방법이 (PLS)
PCA는 또한 데이터 비율어화에 대한 도구로써 사용되고 한다
Principal Component란 무엇인가
2차원의 scatter plot을 이용하여 데이터간의 관계를 보통 확인하는데 p=10일 경우, 그려지는 그래프만 45개에 달한다. 또한 각각의 그래프 또한 딱히 중요하지는 않을텐데 이는 각각의 그래프가 나타내는것이 총 데이터에서 일부분에 지나지 않기 때문이다. 즉 우리가 2차원의 그래프를 그릴때, 해당 변수가 데이터에 대해 가장 영양가 있는 (informative) 상황이라면 우리는 큰 데이터를 더 낮은 차원의 공간에서 관찰할 수 있게 되는것이다. (즉 데이터에 대해 가장 잘 나타내는 변수만 관찰하면 파악하기 쉬우니까)
PCA provides a tool to do just this. It finds a low-dimensional representation of a data set that contains as much as possible of the variation. 여러개의 변수중에 흥미로운 변수 (차원들)을 파악하려고 노력하는데 이는 관련 변수의 observations가 각 차원에서 얼마나 vary하는가를 기준으로 한다.

계수로 인한 분산이 무한이 커지는것을 막기위해 합을 1로 제한한다.
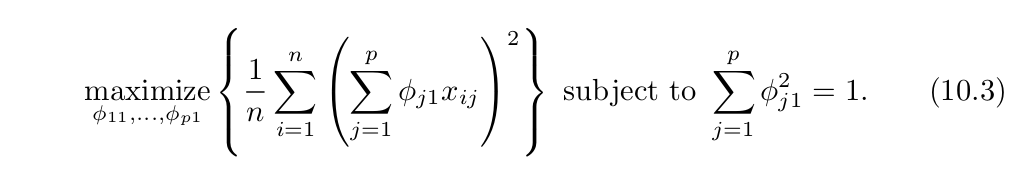
기존의 데이터셋에 공분산 행렬을 생성하고 (괄호 안), 고유의 Vector와 값을 계산 (대괄호). 그런 다음에 고유 값이 큰 순서대로 정렬 후 변환해야할 차원의 수 만큼 고유 값을 정한 뒤. 고유 Vector에 투영하여 차원을 축소한다.
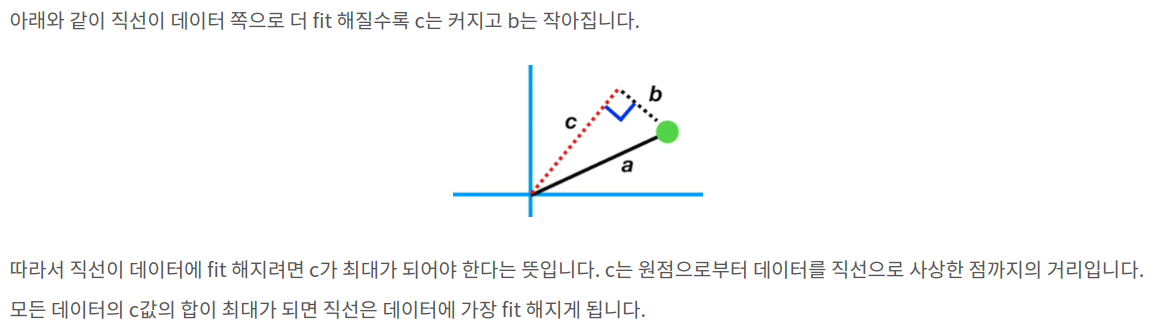
머신러닝 - 9. 차원 축소와 PCA (Principal Components Analysis)
variance가 maxmized 될때 데이터 클라우드에 가장 가까운 이유가 이 때문. variance가 maxmized 되어야 information loss를 최소화 할 수 있다.
1st Principal Component (PC1) 은 주어진 변수들 중에서 데이터를 강 잘 설명하는 성분이다. 만약 PC1의 기울기가 0.25라면, feature 1 increases 4 then feature 2 increases 1 의 선형 결합이 (Linear Combinaito) 해당 데이터를 가장 잘 설명하는 요소라는 의미가 된다.
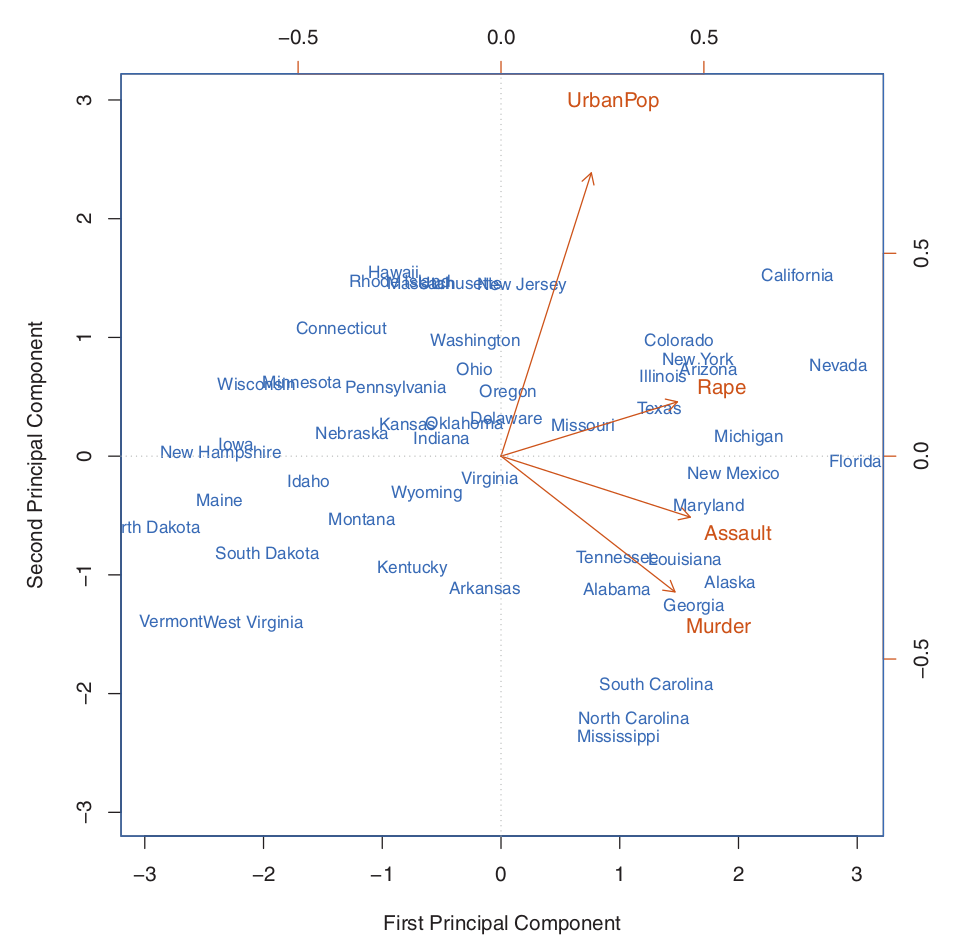
위의 그래프에서 PC1은 Rape Assault Murder에 가중치를 더 부여하고, PC2는 UrbanPop에 더 가중치를 주는것을 볼 수 있다. 따라서 UrbanPop은 변수들이 설명하고자 하는 도시화에 대해 roughly corresponding 한다고 볼 수 있다. 전체적으로, 범죄와 관련된 변수들이 서로 가까이 있으며, 인구수는 이들과 동떨어져있다. 이는 범죄와 관련된 변수들은 서로 correlated되어 있음을 의미한다.
위의 그래프로부터 다음과 같이 해석될 수 있다. 버지니아와 인디애나 같은 주들은 평균치에 가까운 범죄율과 도시화를 가지고 있고, 캘리포니아는 높은 범죄율과 높은 도시율을 가지고 있다고 본다. 이에 비해 하와이는 낮은 범죄율을 가지면서 높은 도시율을 가졌다.
Another Interpretation of Principal Components
위 섹션에서는 PCA를 이용한 시각화 그래프에 대해 variance 최대화에 초점을 맞추었는데. PC1의 로딩 벡터는 또다른 특별한 특징을 가지고 있다: p 차원의 공간에서 n개의 관측점에 대해 가장 가까운 선이라는것. 이 해석이 말하고자 하는것은 매우 분명한데 이는 “모든 데이터에 대해 가장 가깝게 그려진 일 차원 데이터를 찾는데, 이는 이 선이 모든 데이터에 대해 좋은 요약을 해줄것이기 때문” 물론 반드시 일 차원 데이터를 찾는것은 아니다 (적을수록 좋다는것)
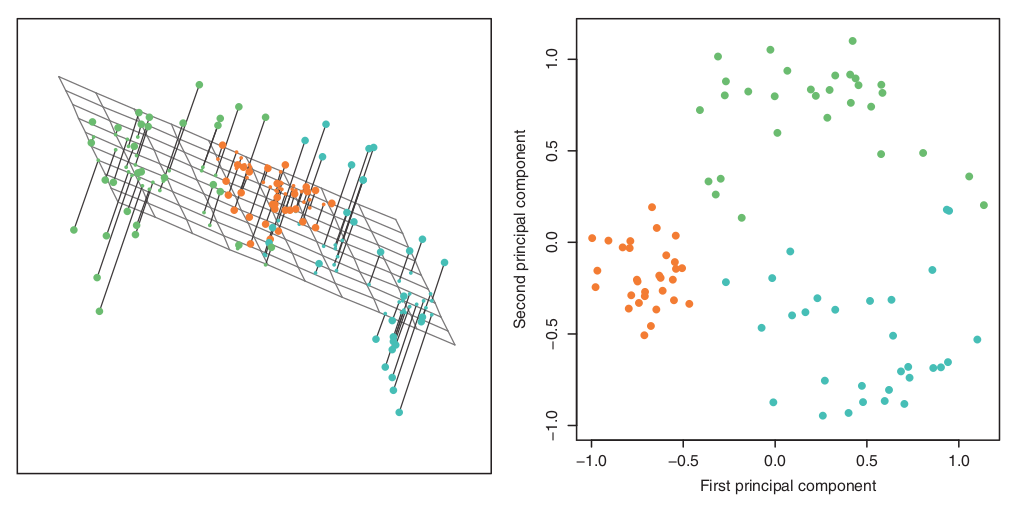
90개의 샘플에 대하여 왼쪽은 삼차원, 오른쪽은 이차원으로 나타낸것이다. 즉 오른쪽에 대해 한 차원을 더 포함한 (third PC) 상태.

More on PCA
변수들 스케일링 하기.
위에서 우리는 PCA를 하기전에 변수들의 평균이 0이 되도록 센터링 시켜야 한다고 하였다. 이에 더불어서 우리가 PCA를 통해 도출한 결과값은 변수들이 각각 얼마나 스케일 되었는지에 대하여 dependant 하다. 이는 다른 supervised & unsupervised 와 차이점으로 존재한다 (다른 방법들은 스케일링으로 인한 결과값이 변하지 않는다).
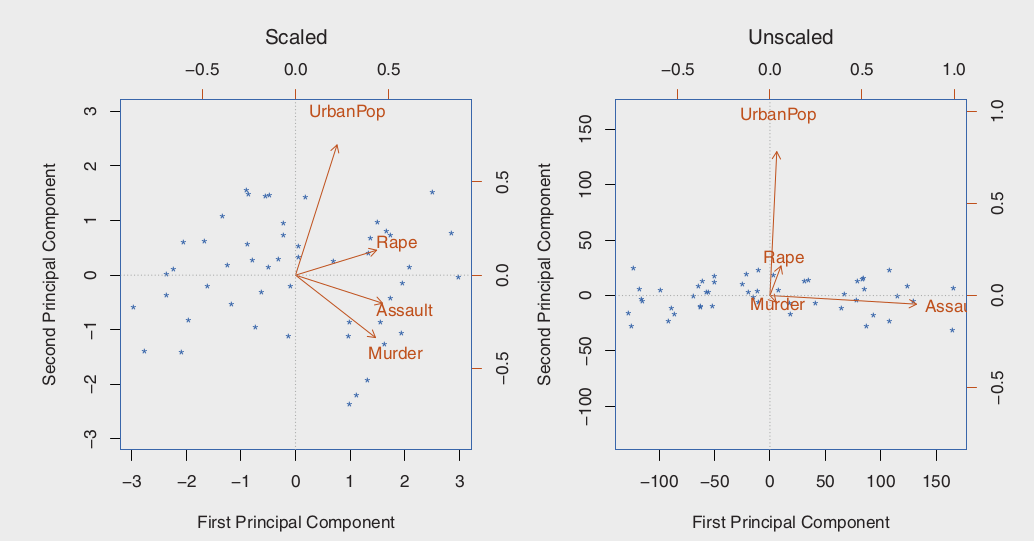
왼쪽의 경우 위와 같이 SD의 총합이 1이 되도록 scaling 한 상태. 오른쪽에서 Assault가 PC1에서 가장 큰 로딩을 가지고 있는데 이는 다른 변수들에 비해 가장 높은 분산을 가지고 있기때문이다. 또한 각 변수들의 unit 또한 각기 다르기 때문에 (100명당 하나, 1000명당 하나, 돈의 경우 1000달러 등등) 그냥 기본적으로 SD를 1로 설정하는 방식이 추천된다.
These four variables have variance 18.97, 87.73, 6945.16, and 209.5, respectively. Consequently, if we perform PCA on the unscaled variables, then the first principal component loading vector will have a very large loading for Assault , since that variable has by far the highest variance.
만약, 모든 변수들이 같은 unit으로 측정되었다면, SD를 1로 하지 않는게 좋다.
Uniqueness of the Principal Components
Each PC loading vector는 고유하다. 이 로딩 벡터의 사인 (플마)는 바뀔지 언정 값 자체는 어느 소프트웨어 패키지에서 실행하던지 같다. 또한 이 사인의 변동또한 의미가 없는것이 결국 방향을 이용하여 분석하기 때문. 따라서 loading vector, and score vector 가 동시에 사인이 바뀌는 이상 최종 결론에는 문제가 없다. (하나만 바뀌고 그러면 안됨)
Proportion of Variance Explained
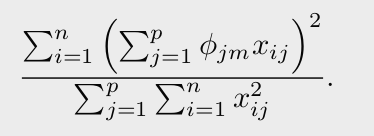

위와 같은 방식으로 각각의 PC가 얼마만큼의 분산을 설명하는지에 대하여 알 수 있지만, 어느선에서 얼마정도의 PC가 필요한가? 에 대한 사항은 특별히 정해진게 없다. scree plot (각각의 PC의 분산 설명도 그래프) 을 이용하여 elbow 를 이용하여 정할수도 있긴 하다. 현실적으로, 혹은 실증적으로는, 우리는 첫 몇몇의 PC를 시각화해서 특이한 패턴이 있는지 확인 하는 식으로 결정한다. 당연하게도, 이러한 방식의 접근은 매우 주관적이며 이로 인해 우리는 PCA는 exploratory data analysis를 위한 시각화 도구로 사용하는 이유중 하나다.
물론 PCA를 supervised에 사용한다면, CV와 같은 방법을 이용하여 score vectors 를 regresisson 튜닝 패러미터로 사용된다면, 몇개의 PC가 사용되어야 하는지 알 수 있다 (왜냐면 이걸 지금 어디에 쓰는지 우리가 분명하게 알고있으니까)


