
Reference :
- Introduction to Parallel Computing, Edition Second by Vipin Kumar et al
- The Australian National University CECS
Granularity
- Granularity: size of the tasks
- Coarse grain: large tasks/many instructions
- Fine grain: small tasks/few instructions
- Metric = t_compute / t_communication
- It may depend on number of processors.
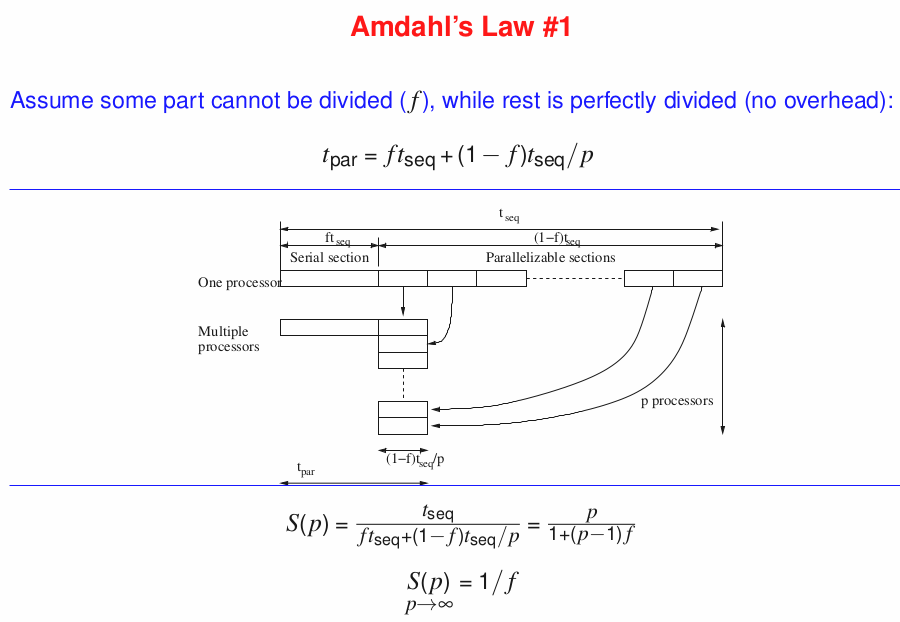
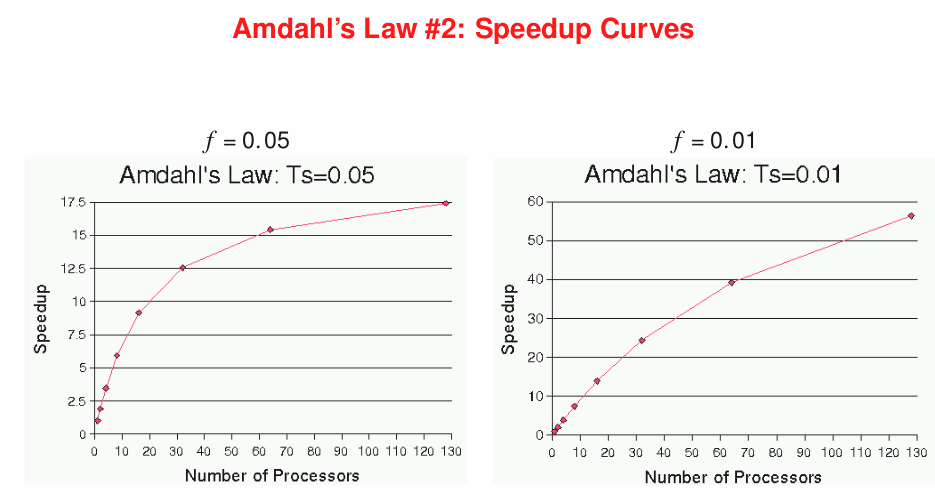
Speedup
- the relative performance between single and multiple processors
- ⇒ S(n) = exe time on single / exe time on p = t_seq / t_par
- t_seq should be the fastest known sequential algo; best parallel algo may be differernt
- S_operation(p) = operation count rate with p / operation count rate on single
- Linear speedup = max possible S(n) = p
- if S(P) > P then
- May imply the algo is not the best one, go and check the seq algo
- May arise due to the unique feature of architecture.
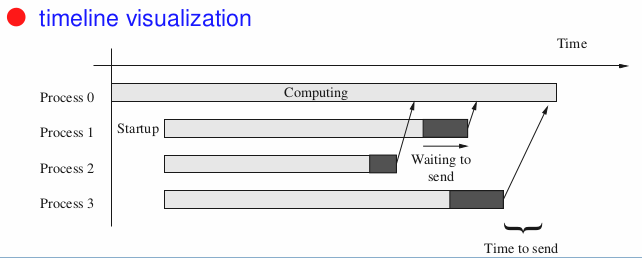
Parallel Overhead
- Factors that limit parallel scalability:
- periods that not all p works + time when one p is active on seq parts
- load imbalance
- extra computations not in the seq code —> seq code in one p might be faster some cases
- communication times
Efficiency and Cost
- Efficiency: How well using the processors
$$E = t_{seq} / t_{par} / p = S(p)/p * 100%$$
- Cost: parallel execution time * total num of p
- Cost optimal = cost has same asymptotic growth as a func of input size as the fastest seq algo on a single processor
$$cost = t_{par} * p = (t_{seq}*p)/S(p) = t_{seq} / E$$
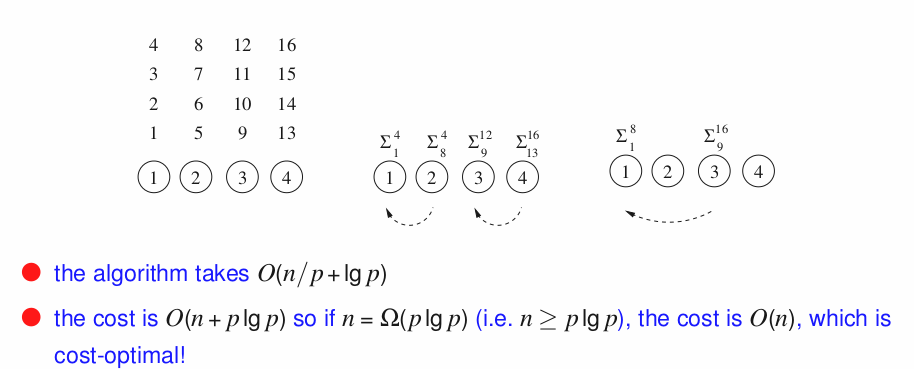
Adding n num on n processors
Adding n in a single core = n; adding n in n processor = lg(n). Therefore speedup = O(n/lg(n))
cost = number of p * time of execution = n * lg(n) = O(n lg(n))
Hence it is not cost-optimal
Scalability
Imprecise measure:
- hardware: 하드웨어를 늘리면 퍼포먼스가 좋아지나?
- 링, 크로스바, 하이퍼큐브 위상을 고려하고 프로세서에 무슨 변화를 줘야 하는지 고려
- Algorithm: 사용하고 있는 알고리즘이 더 많은 프로세서와 accomodate 가능 한가?
- Combined: 문제 크기 증가를 프로세서를 증가함으로써 accomodate 가능 한가?
- 계산 사이즈를 배로 늘렸을때의 변화를 고려
- N*N 매트릭스의 N사이즈를 두배로 늘리면, 더하기 계산의 비용은 4배지만 곱하기 비용은 8배로 늘어난다



